
【题目】已知在几何体中,四边形![]() 是边长为
是边长为![]() 的正方形,且
的正方形,且![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1) 取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,结合已知条件证得
,结合已知条件证得![]() 平面
平面![]() ,由勾股定理得
,由勾股定理得![]() ,利用定理证得结果
,利用定理证得结果![]() 以点
以点![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系,求平面
轴,建立如图所示的空间直角坐标系,求平面![]() 的法向量为
的法向量为![]() ,求平面
,求平面![]() 的法向量为
的法向量为![]() ,运用公式求出结果
,运用公式求出结果
解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,
∵![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() 为
为![]() 与平面
与平面![]() 所成的角.
所成的角.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,设
,设![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() .∴平面
.∴平面![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() ,
,![]() 两两垂直,以点
两两垂直,以点![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
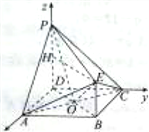
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则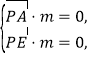 即
即![]() 取
取![]() ,
,
得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
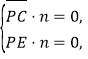 即
即![]()
取![]() ,得
,得![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,
,
∵![]()
![]() ,
,
∴![]() ,即二面角
,即二面角![]() 的大小为
的大小为![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
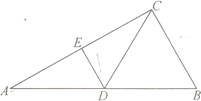

如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 命题![]() 的否定是:
的否定是:![]()
B. 命题![]() 中,若
中,若![]() ,则
,则![]() 的否命题是真命题
的否命题是真命题
C. 如果![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() 为真命题,
为真命题,![]() 为假命题
为假命题
D. ![]() 是函数
是函数![]() 的最小正周期为
的最小正周期为![]() 的充分不必要条件
的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.

(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点与双曲线
的焦点与双曲线![]() 的焦点重合,过椭圆
的焦点重合,过椭圆![]() 的右顶点
的右顶点![]() 任意作直线
任意作直线![]() ,交抛物线
,交抛物线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)试求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的左焦点
的左焦点![]() 作互相垂直的两条直线,分别交椭圆
作互相垂直的两条直线,分别交椭圆![]() 于点
于点![]() 、
、![]() 、
、![]() 、
、![]() ,试求四边形
,试求四边形![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题14分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.
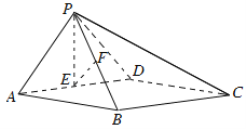
(Ⅰ)求证:PE⊥BC;
(Ⅱ)求证:平面PAB⊥平面PCD;
(Ⅲ)求证:EF∥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足以下三个条件:
满足以下三个条件:
①对任意实数![]() ,都有
,都有![]() ;
;
②![]() ;
;
③![]() 在区间
在区间![]() 上为增函数.
上为增函数.
(1)判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)求证:![]() ;
;
(3)解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com