
| A. | 4 | B. | $\sqrt{10}$ | C. | $\sqrt{19}$ | D. | 25 |
分析 根据向量坐标,结合数量积的定义求出相应的长度和夹角.
解答 解:∵$\overrightarrow{AB}$=(2cosα,2sinα),$\overrightarrow{BC}$=(5cosβ,5sinβ),
∴|$\overrightarrow{AB}$|=2,|$\overrightarrow{BC}$|=5,
∵$\overrightarrow{AB}$•$\overrightarrow{BC}$=-5,
∴$\overrightarrow{BA}$?$\overrightarrow{BC}$=5,
∴cos∠ABC=cos<$\overrightarrow{BA}$,$\overrightarrow{BC}$>=$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BA}|•|BC|}$=$\frac{5}{2×5}$=$\frac{1}{2}$,
∴${\overrightarrow{AC}}^{2}$=22+52-2×2×5×cos∠ABC=19,
故|$\overrightarrow{AC}$|=$\sqrt{19}$,
故选:C.
点评 本题主要考查平面向量数量积的应用,要求熟练掌握利用数量积求向量夹角和向量长度.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 现在阳台种菜成为部分人的爱好,如图所示,一块种菜的小菜地一面靠墙(墙长度为1.2米),另外三面由总长为2米的栅栏围成,设宽为x米.面积为y平方米.
现在阳台种菜成为部分人的爱好,如图所示,一块种菜的小菜地一面靠墙(墙长度为1.2米),另外三面由总长为2米的栅栏围成,设宽为x米.面积为y平方米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
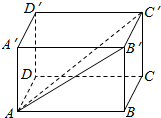 如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:
如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | M?N | C. | M=N | D. | M∩N=∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com