
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.

(1)设G,H分别为PB,AC的中点,求证:GH//平面PAD;
(2)求证:![]() ⊥平面PCD;
⊥平面PCD;
(3)求直线AD与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定![]() 考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式
考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式![]() 随着金融业的发展,普通人能够使用的投资理财工具也多了起来
随着金融业的发展,普通人能够使用的投资理财工具也多了起来![]() 为了研究某种理财工具的使用情况,现对
为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组:
年龄段的人员进行了调查研究,将各年龄段人数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
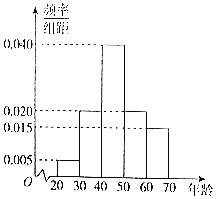
![]() Ⅰ
Ⅰ![]() 估计使用这种理财工具的人员年龄的中位数、平均数;
估计使用这种理财工具的人员年龄的中位数、平均数;
![]() Ⅱ
Ⅱ![]() 采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
![]() Ⅲ
Ⅲ![]() 在
在![]() Ⅱ
Ⅱ![]() 中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点所形成的图形是圆.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系
的点所形成的图形是圆.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 满足
满足![]() .设点
.设点![]() 所构成的曲线为
所构成的曲线为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的方程为
的方程为![]()
B.在![]() 上存在点
上存在点![]() ,使得
,使得![]() 到点
到点![]() 的距离为
的距离为![]()
C.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
D.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场亲子游乐场由于经营管理不善突然倒闭.在进行资产清算时发现有3000名客户办理的充值会员卡上还有余额.为了了解客户充值卡上的余额情况,从中抽取了300名客户的充值卡余额进行统计.其中余额分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
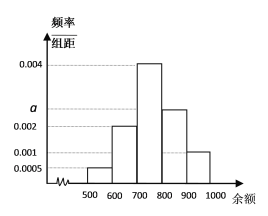
(1)求![]() 的值;
的值;
(2)求余额不低于![]() 元的客户大约为多少人?
元的客户大约为多少人?
(3)根据频率分布直方图,估计客户人均损失多少?(用组中值代替各组数据的平均值).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com