
����Ŀ�������ĸ��жϣ� ��ijУ����һ���������������ֱ���m��n��ij�β�����ѧƽ���ֱַ���a��b���������������ѧƽ����Ϊ ![]() ��
��
��10������ij������ͬһ����ļ����ֱ���15��17��14��10��15��17��17��16��14��12������ƽ����Ϊa����λ��Ϊb������Ϊc������c��a��b��
�۴������г�ȡ������Ϊ ![]() ����ع�ֱ��
����ع�ֱ�� ![]() �ع��㣨
�ع��㣨 ![]() ��
��
����֪�η�����̬�ֲ�N��0����2������P����2�ܦΡ�0��=4����P���Σ�2��=0.2
������ȷ�ĸ����У� ��
A.4��
B.3��
C.2��
D.1��
���𰸡�D
���������⣺��������ɵ������������ѧƽ����Ϊ ![]() ���ʢٴ�����������ɵ�a=
���ʢٴ�����������ɵ�a= ![]() ��15+17+14+10+15+17+17+16+14+12��=14.7��b=15��c=17��
��15+17+14+10+15+17+17+16+14+12��=14.7��b=15��c=17��
����c��b��a���ʢڴ����������Իع鷽�̵��ص㣬�ɵûع�ֱ�� ![]() �ع��������ĵ㣨
�ع��������ĵ㣨 ![]() �����ʢ۶ԣ�����֪�η�����̬�ֲ�N��0����2������P����2�ܦΡ�0��=0.4����P���Σ���2��=0.5��0.4=0.1��
�����ʢ۶ԣ�����֪�η�����̬�ֲ�N��0����2������P����2�ܦΡ�0��=0.4����P���Σ���2��=0.5��0.4=0.1��
��P���Σ�2��=P���Σ���2��=0.1���ʢܴ���
��ѡ��D��
�����㾫����������Ĺؼ������������������ж���Ӧ�õ����֪ʶ�������������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����an= ![]() ������{an}����ȡһ������Ϊq�ĵȱ�����{a
������{an}����ȡһ������Ϊq�ĵȱ�����{a ![]() }������k1=1��k1��k2������kn �� kn��N*����������������Сq��ֵΪ�� ��
}������k1=1��k1��k2������kn �� kn��N*����������������Сq��ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=logax��x��2 ʱ����|y|��1����a��ȡֵ��Χ�ǣ� ��
A.![]()
B.![]()
C.1��a��2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫ263�����ң��ҹ���ѧ�����շ��ֵ�Բ�ڽ�������εı�����������ʱ������ε���������ޱƽ�Բ��������������ˡ���Բ���������á���Բ�������յõ���Բ���ʾ�ȷ��С�������λ�Ľ���ֵ3.14������������ġ����ʡ�����ͼ���������յġ���Բ����˼����Ƶ�һ�������ͼ������n��ʾԲ�ڽ�������εı�����ִ�д��㷨�����Բ���ʵĽ���ֵ����Ϊ���ο����ݣ� ![]() ��1.732��sin15���0.2588��sin75���0.1305���� ��
��1.732��sin15���0.2588��sin75���0.1305���� �� 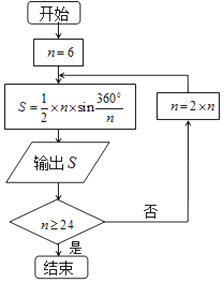
A.2.598��3��3.1048
B.2.598��3��3.1056
C.2.578��3��3.1069
D.2.588��3��3.1108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ������y=f��x���ڵ㣨e2 �� f��e2��������������ֱ��2x+y=0��ֱ������eΪ��Ȼ�����ĵ�������
������y=f��x���ڵ㣨e2 �� f��e2��������������ֱ��2x+y=0��ֱ������eΪ��Ȼ�����ĵ�������
��1����f��x���Ľ���ʽ�������ݼ����䣻
��2��������x0��[e��+�ޣ���ʹ����g��x��=aelnx+ ![]() lnxf��x����a��������ʵ��a��ȡֵ��Χ��
lnxf��x����a��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����ڳ�Ϊ8km�ĵ�·OP��һ����һ���˶�������������ǰһ����Ϊ���߶�OSM�������߶�Ϊ����y=Asin��x��A��0���أ�0��x��[0��4]��ͼ����ͼ�����ߵ�Ϊ ![]() �������ĺ�һ����Ϊ���߶�MNP��Ϊ��֤�����˶�Ա�İ�ȫ������MNP=120��
�������ĺ�һ����Ϊ���߶�MNP��Ϊ��֤�����˶�Ա�İ�ȫ������MNP=120�� 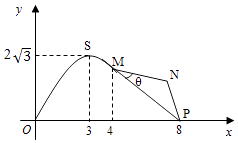
��1����A���ص�ֵ��M��P�����ľ��룻
��2��Ӧ�����ƣ�����ʹ���߶�����MNP���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У���֪��A��0��3����B��6��0����
�������߶�AB��ֱƽ���ߵķ��̣�
����������C�ϵ�����һ��P����2|PA|��|PB|��������C�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ�����R�ϵ��溯������f��x+2��=f��x��2������0��x��1ʱ��f��x��= ![]() ����f��1��+f��2��+f��3��+��+f���ڣ� ��
����f��1��+f��2��+f��3��+��+f���ڣ� ��
A.��1
B.0
C.1
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y2��4x���ڽ������ε�һ��������ԭ�㣬�����ϵĸ��߶�ͨ�������ߵĽ��㣬������������Բ�ķ��̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com