
【题目】已知f(x)=x2﹣a|x﹣1|+b(a>0,b>﹣1)
(1)若b=0,a>2,求f(x)在区间[0,2]内的最小值m(a);
(2)若f(x)在区间[0,2]内不同的零点恰有两个,且落在区间[0,1),(1,2]内各一个,求a﹣b的取值范围.
【答案】
(1)解:b=0,a>2时,f(x)=x2﹣a|x﹣1|,
当0≤x≤1时,f(x)=x2+ax﹣a,且在[0,1]递增,
可得f(0)取得最小值﹣a;
当1<x≤2时,f(x)=x2﹣ax+a, ![]() >1,
>1,
当a>4时, ![]() >2,在(1,2]递减,可得最小值f(2)=4﹣a;
>2,在(1,2]递减,可得最小值f(2)=4﹣a;
当2<a≤4时,1< ![]() ≤2,可得f(
≤2,可得f( ![]() )取得最小值,且为a﹣
)取得最小值,且为a﹣ ![]() .
.
由﹣a<4﹣a,a﹣ ![]() ﹣(﹣a)=
﹣(﹣a)= ![]() >0(2<a≤4),
>0(2<a≤4),
即有a﹣ ![]() >﹣a.
>﹣a.
综上可得,m(a)=﹣a;
(2)解:由f(x)= ![]() ,
,
当0≤x<1时,f(x)递增,可得f(0)f(1)≤0,
即为(b﹣a)(1+b)≤0①
当1<x≤2时,f(x)有一个零点,可得f(1)f(2)≤0或f( ![]() )=0(2<a≤4),
)=0(2<a≤4),
即为(1+b)(4﹣a+b)≤0或b= ![]() ﹣a②
﹣a②
由 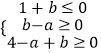 或
或 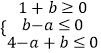 或a﹣b=
或a﹣b= ![]() (2<a≤4),
(2<a≤4),
可得a﹣b≤0或a﹣b≥4或3<a﹣b≤4,
综上可得a﹣b的范围是(﹣∞,0]∪(3,+∞)
【解析】(1)讨论当0≤x≤1时,当1<x≤2时,同时对a讨论,可得f(x)的单调性,可得最小值;(2)将f(x)写成分段函数式,讨论当0≤x<1时,当1<x≤2时,由函数的零点存在定理,可得不等式组,解不等式即可得到所求范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图.

(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的中点值作为代表);
(2)根据已知条件完成下面的2×2列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附:参考公式![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)证明: ![]() ;
;
(Ⅱ)若棱锥![]() 的体积为
的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】【试题分析】(I) 取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .利用等腰三角形的性质和矩形的性质可证得
.利用等腰三角形的性质和矩形的性质可证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,故
,故![]() ,故
,故![]() .(II) 可知
.(II) 可知![]() 是棱锥的高,利用体积公式求得
是棱锥的高,利用体积公式求得![]() ,利用勾股定理和等腰三角形的性质求得
,利用勾股定理和等腰三角形的性质求得![]() 的值,进而求得面积.
的值,进而求得面积.
【试题解析】
证明:(Ⅰ)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
底面![]() 中,可得四边形
中,可得四边形![]() 为矩形,∴
为矩形,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,所以
,所以![]() .
.
(Ⅱ)由面![]() 面
面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,所以
,所以![]() 为棱锥
为棱锥![]() 的高,
的高,
由![]() ,知
,知![]() ,
,
![]()
![]()
![]() ,
,
∴![]() .
.
由(Ⅰ)知![]() ,
,![]() ,∴
,∴![]() .
.
![]() .
.
由![]() ,可知
,可知![]() 平面
平面![]() ,∴
,∴![]() ,
,
因此![]() .
.
在![]() 中
中![]() ,
,![]() ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,
,![]() ,
,
∴![]()
![]() .
.
所以棱锥![]() 的侧面积为
的侧面积为![]() .
.
【题型】解答题
【结束】
20
【题目】已知圆![]() 经过椭圆
经过椭圆![]() :
: ![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,它们在
上的两点,它们在![]() 轴两侧,且
轴两侧,且![]() 的平分线在
的平分线在![]() 轴上,
轴上, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A1 , A2 , A3 , …,An是集合{1,2,3,…,n}的n个非空子集(n≥2),定义aij= ![]() ,其中i,j=1,2,…,n,这样得到的n2个数之和记为S(A1 , A2 , A3 , …,An),简记为S,下列三种说法:①S与n的奇偶性相同;②S是n的倍数;③S的最小值为n,最大值为n2 . 其中正确的判断是( )
,其中i,j=1,2,…,n,这样得到的n2个数之和记为S(A1 , A2 , A3 , …,An),简记为S,下列三种说法:①S与n的奇偶性相同;②S是n的倍数;③S的最小值为n,最大值为n2 . 其中正确的判断是( )
A.①②
B.①③
C.②③
D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1底面是边长为1的正方形,高AA1= ![]() ,点A是平面α内的一个定点,AA1与α所成角为
,点A是平面α内的一个定点,AA1与α所成角为 ![]() ,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= .
,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=r2(r>0)与直线l:y=x+3,且直线l有唯一的一个点P,使得过P点作圆C的两条切线互相垂直,则r=;设EF是直线l上的一条线段,若对于圆C上的任意一点Q,∠EQF≥ ![]() ,则|EF|的最小值= .
,则|EF|的最小值= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解某地区电视观众对某类体育节目的收视情况随机抽取了100名观众进行调查,其中女性有55名.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
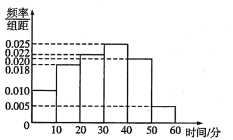
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别有关?
列联表,并据此资料你是否认为“体育迷”与性别有关?
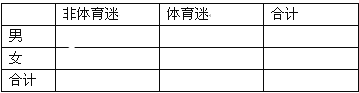
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域
的定义域![]() ,值域是
,值域是![]() ;
;![]() 定义域
定义域![]() ,值域是
,值域是![]() ,其中实数
,其中实数![]() 满足
满足![]() .
.
甲:如果任意![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
乙:如果存在![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丙:如果任意![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丁:如果存在![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
请判断上述四个命题中,假命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com