
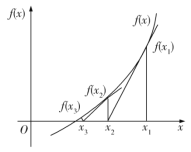
【题目】牛顿迭代法(Newton's method)又称牛顿–拉夫逊方法(Newton–Raphsonmethod),是牛顿在17世纪提出的一种近似求方程根的方法.如图,设![]() 是
是![]() 的根,选取
的根,选取![]() 作为
作为![]() 初始近似值,过点
初始近似值,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 与
与![]() 轴的交点的横坐标
轴的交点的横坐标![]() ,称
,称![]() 是
是![]() 的一次近似值,过点
的一次近似值,过点![]() 作曲线
作曲线![]() 的切线,则该切线与
的切线,则该切线与![]() 轴的交点的横坐标为
轴的交点的横坐标为![]() ,称
,称![]() 是
是![]() 的二次近似值.重复以上过程,直到
的二次近似值.重复以上过程,直到![]() 的近似值足够小,即把
的近似值足够小,即把![]() 作为
作为![]() 的近似解.设
的近似解.设![]() 构成数列
构成数列![]() .对于下列结论:
.对于下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中正确结论的序号为__________.
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若x2=1,则x≠1”的否命题是“若x2=1,则x=1”
B. 命题“![]() ”的否定是“x∈R,x2﹣x>0”
”的否定是“x∈R,x2﹣x>0”
C. “y=f(x)在x0处有极值”是“f'(x0)=0”的充要条件
D. 命题“若函数f(x)=x2﹣ax+1有零点,则“a≥2或a≤﹣2”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() .
.
(1)写出抛物线![]() 的标准方程及其准线方程,并求抛物线
的标准方程及其准线方程,并求抛物线![]() 的焦点到准线的距离;
的焦点到准线的距离;
(2)过点![]() 且斜率存在的直线
且斜率存在的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且点
,且点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(i)求点![]() 的坐标;
的坐标;
(ii)求![]() 与
与![]() 面积之和的最小值.
面积之和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,则下列说法中不正确的是( )
A.由样本数据得到的回归方程![]() 必过样本点的中心
必过样本点的中心![]() .
.
B.残差平方和越小的模型,拟合的效果越好.
C.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 的值越小,说明模型的拟合效果越好.
的值越小,说明模型的拟合效果越好.
D.回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年上半年我国多个省市暴发了“非洲猪瘟”疫情,生猪大量病死,存栏量急剧下降,一时间猪肉价格暴涨,其他肉类价格也跟着大幅上扬,严重影响了居民的生活.为了解决这个问题,我国政府一方面鼓励有条件的企业和散户防控疫情,扩大生产;另一方面积极向多个国家开放猪肉进口,扩大肉源,确保市场供给稳定.某大型生猪生产企业分析当前市场形势,决定响应政府号召,扩大生产,决策层调阅了该企业过去生产相关数据,就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表:
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究员甲根据以上数据认为![]() 与
与![]() 具有线性回归关系,请帮他求出
具有线性回归关系,请帮他求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (保留小数点后两位有效数字)
(保留小数点后两位有效数字)
(2)研究员乙根据以上数据得出![]() 与
与![]() 的回归模型:
的回归模型:![]() .为了评价两种模型的拟合结果,请完成以下任务:
.为了评价两种模型的拟合结果,请完成以下任务:
①完成下表(计算结果精确到0.01元)(备注:![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 | |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估计值 | |||||
残差 | ||||||
模型乙 | 估计值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
残差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 与
与![]() 的大小,判断哪个模型拟合效果更好;
的大小,判断哪个模型拟合效果更好;
(3)根据市场调查,生猪存栏数量达到1万头时,饲养一头猪每一天的平均收入为7.5元;生猪存栏数量达到1.2万头时,饲养一头猪每一天的平均收入为7.2元.若按(2)中拟合效果较好的模型计算一天中一头猪的平均成本,问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.(利润=收入-成本)
参考公式: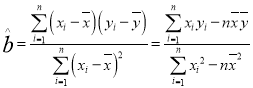 ,
,![]()
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是常数).
是常数).
(1)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(2)若![]() 为奇函数,求实数
为奇函数,求实数![]() .并证明
.并证明![]() 的图像始终在
的图像始终在![]() 的图像的下方;
的图像的下方;
(3)设函数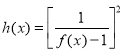 ,若对任意
,若对任意![]() ,以
,以![]() 为边长总可以构成三角形,求
为边长总可以构成三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com