已知:点P与点F(2,0)的距离比它到直线x+4=0的距离小2,若记点P的轨迹为曲线C.
(1)求曲线C的方程.
(2)若直线L与曲线C相交于A、B两点,且OA⊥OB.求证:直线L过定点,并求出该定点的坐标.
(3)试利用所学圆锥曲线知识参照(2)设计一个与直线L过定点有关的数学问题,并解答所提问题.
【答案】
分析:(1)解法(A):点P与点F(2,0)的距离比它到直线x+4=0的距离小2,所以点P与点F(2,0)的距离与它到直线x+2=0的距离相等.由抛物线定义得:点P在以F为焦点直线x+2=0为准线的抛物线上,由此能求出抛物线方程.
解法(B):设动点P(x,y),则
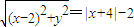
.当x≤-4时,(x-2)
2+y
2=(-x-6)
2,此时曲线不存在.当x>-4时,(x-2)
2+y
2=(x+2)
2,化简得:y
2=8x.
(2)设直线L:y=kx+b与抛物线交予点(x
1,y
1),(x
2,y
2),(a)若L斜率存在,设为k,
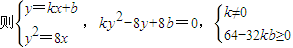
,
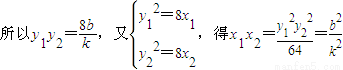
,由此能导出直线为y=k(x-8),所以L过定点(8,0).
(3)(逆命题)如果直线L过定点(8,0),且与抛物线y
2=8x相交于A、B两点,O为坐标原点.求证:
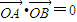
.
证明:设其方程为y=k(x-8),设A(x
1,y
1),B(x
2,y
2),联立方程组
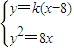
,消去y,并整理得k
2x
2-(16k
2+8)x+64k
2=0,
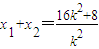
,x
1x
2=64,y
1y
2=k(x
1-8)•k(x
2-8)=k
2x
1x
2-8k
2(x
1+x
2)+64k
2=-64.所以
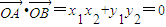
.
解答:解:(1)解法(A):点P与点F(2,0)的距离比它到直线x+4=0的距离小2,所以点P与点F(2,0)的距离与它到直线x+2=0的距离相等.(1分)
由抛物线定义得:点P在以F为焦点直线x+2=0为准线的抛物线上,(1分)
抛物线方程为y
2=8x.(2分)
解法(B):设动点P(x,y),则
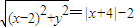
.
当x≤-4时,(x-2)
2+y
2=(-x-6)
2,
化简得:y
2=8(x+2),显然x≥-2,而x≤-4,此时曲线不存在.
当x>-4时,(x-2)
2+y
2=(x+2)
2,化简得:y
2=8x.
(2)设直线L:y=kx+b与抛物线交予点(x
1,y
1),(x
2,y
2),(a)若L斜率存在,设为k,,
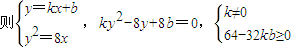
,(1分)
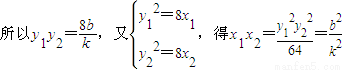
,

,即
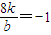
,b=-8k,(2分)
直线为y=k(x-8),所以L过定点(8,0)(1分)
(3)(逆命题)如果直线L过定点(8,0),且与抛物线y
2=8x相交于A、B两点,O为坐标原点.求证:
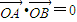
.
证明:∵直线L过定点(8,0),
∴设其方程为y=k(x-8),设A(x
1,y
1),B(x
2,y
2),
联立方程组
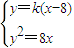
,消去y,并整理得k
2x
2-(16k
2+8)x+64k
2=0,
∴
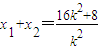
,x
1x
2=64,
y
1y
2=k(x
1-8)•k(x
2-8)
=k
2x
1x
2-8k
2(x
1+x
2)+64k
2=-64.
∴
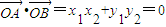
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,解题时要注意合理地进行等价转化.

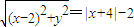 .当x≤-4时,(x-2)2+y2=(-x-6)2,此时曲线不存在.当x>-4时,(x-2)2+y2=(x+2)2,化简得:y2=8x.
.当x≤-4时,(x-2)2+y2=(-x-6)2,此时曲线不存在.当x>-4时,(x-2)2+y2=(x+2)2,化简得:y2=8x.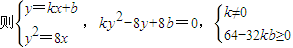 ,
,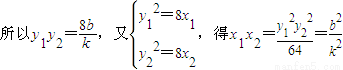 ,由此能导出直线为y=k(x-8),所以L过定点(8,0).
,由此能导出直线为y=k(x-8),所以L过定点(8,0).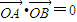 .
. 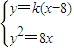 ,消去y,并整理得k2x2-(16k2+8)x+64k2=0,
,消去y,并整理得k2x2-(16k2+8)x+64k2=0,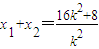 ,x1x2=64,y1y2=k(x1-8)•k(x2-8)=k2x1x2-8k2(x1+x2)+64k2=-64.所以
,x1x2=64,y1y2=k(x1-8)•k(x2-8)=k2x1x2-8k2(x1+x2)+64k2=-64.所以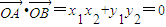 .
.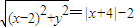 .
.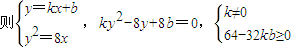 ,(1分)
,(1分)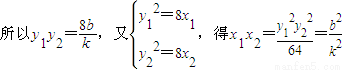 ,
, ,即
,即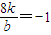 ,b=-8k,(2分)
,b=-8k,(2分)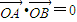 .
. 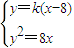 ,消去y,并整理得k2x2-(16k2+8)x+64k2=0,
,消去y,并整理得k2x2-(16k2+8)x+64k2=0,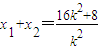 ,x1x2=64,
,x1x2=64,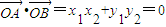 .
.
