
【题目】为了解高校学生平均每天使用手机的时间长短是否与性别有关,某调查小组随机抽取了25 名男生、10名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机 | 平均每天使用手机 | 合计 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合计 | 18 | 17 | 35 |
(I)在参与调查的平均每天使用手机不超过3小时的7名女生中,有4人使用国产手机,从这7名女生中任意选取2人,求至少有1人使用国产手机的概率;
(II) 根据列联表,是否有90%的把握认为学生使用手机的时间长短与性别有关(![]() 的观测值
的观测值![]() 精确到0.01).
精确到0.01).
附:
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式: 
![]()
科目:高中数学 来源: 题型:
【题目】袋子中有5个大小质地完全相同的球,其中2个红球、3个黄球,从中不放回地依次随机摸出2个球,求下列事件的概率:
(1)A=“第一次摸到红球”;
(2)B=“第二次摸到红球”;
(3)AB=“两次都摸到红球”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人的眼皮有单眼皮与双眼皮之分,这是由对应的基因决定的.生物学上已经证明:决定眼皮单双的基因有两种,一种是显性基因(记为![]() ),另一种是隐性基因(记为
),另一种是隐性基因(记为![]() );基因总是成对出现(如
);基因总是成对出现(如![]() 、
、![]() 、
、![]() 、
、![]() ),而成对的基因中,只要出现了显性基因,那么这个人就一定是双眼皮(也就是说,“单眼皮”的充要条件是“成对的基因是
),而成对的基因中,只要出现了显性基因,那么这个人就一定是双眼皮(也就是说,“单眼皮”的充要条件是“成对的基因是![]() ”);如果不发生基因突变的话,成对的基因中,一个来自父亲,另一个来自母亲,但父母亲提供基因时都是随机的.有一对夫妻,两人成对的基因都是
”);如果不发生基因突变的话,成对的基因中,一个来自父亲,另一个来自母亲,但父母亲提供基因时都是随机的.有一对夫妻,两人成对的基因都是![]() ,不考虑基因突变,求他们的孩子是单眼皮的概率.
,不考虑基因突变,求他们的孩子是单眼皮的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 作与
作与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() .
.
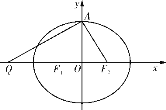
(1)若过![]() ,
,![]() ,
,![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() :
:![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() 使得以
使得以![]() ,
,![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其它各面用钢筋网围成.
(1)现有可围![]() 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为![]() ,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?
,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为O(0,0),焦点F(0,1)
(Ⅰ)求抛物线C的方程;
(Ⅱ)过F作直线交抛物线于A、B两点.若直线OA、OB分别交直线l:y=x﹣2于M、N两点,求|MN|的最小值.
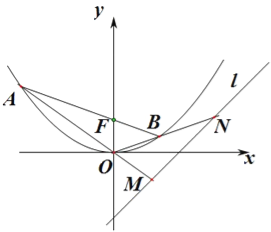
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com