
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】在一个不透明的盒子中,放有标号分别为![]() ,
,![]() ,
,![]() ,
,![]() 的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为
的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为![]() ,
,![]() .
.
(1)求事件![]() 的概率;
的概率;
(2)求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
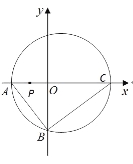
【题目】如图,直角三角形![]() 的顶点坐标
的顶点坐标![]() ,直角顶点
,直角顶点![]() ,顶点
,顶点![]() 在
在![]() 轴上,点
轴上,点![]() 为线段
为线段![]() 的中点,三角形
的中点,三角形![]() 外接圆的圆心为
外接圆的圆心为![]() .
.
(1)求![]() 边所在直线方程;
边所在直线方程;
(2)求圆![]() 的方程;
的方程;
(3)直线![]() 过点
过点![]() 且倾斜角为
且倾斜角为![]() ,求该直线被圆
,求该直线被圆![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发![]() 个红包,每个红包金额为
个红包,每个红包金额为![]() 元,
元,![]() .已知在每轮游戏中所产生的
.已知在每轮游戏中所产生的![]() 个红包金额的频率分布直方图如图所示.
个红包金额的频率分布直方图如图所示.
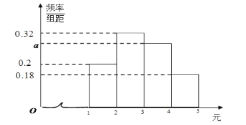
(1)求![]() 的值,并根据频率分布直方图,估计红包金额的众数;
的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在![]() 的红包个数为
的红包个数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如下表:
阅读名著的本数 | 1 | 2 | 3 | 4 | 5 |
男生人数 | 3 | 1 | 2 | 1 | 3 |
女生人数 | 1 | 3 | 3 | 1 | 2 |
(1)试根据上述数据,求这个班级女生阅读名著的平均本数;
(2)若从阅读![]() 本名著的学生中任选
本名著的学生中任选![]() 人交流读书心得,求选到男生和女生各
人交流读书心得,求选到男生和女生各![]() 人的概率;
人的概率;
(3)试比较该班男生阅读名著本数的方差![]() 与女生阅读名著本数的方差
与女生阅读名著本数的方差![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料 ![]() ,五合板
,五合板 ![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料 ![]() ,五合板
,五合板 ![]() ,生产每个书橱需要方木料
,生产每个书橱需要方木料 ![]() ,五合板
,五合板 ![]() ,出售一张书桌可获利润
,出售一张书桌可获利润 ![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润 ![]() 元.
元.
(1)如果只安排生产书桌,可获利润多少?
(2)如果只安排生产书橱,可获利润多少?
(3)怎祥安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在区间![]() 上的函数
上的函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() 成立,那么称函数
成立,那么称函数![]() 在区间
在区间![]() 上可被
上可被![]() 替代,
替代,![]() 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:
①![]() 在区间
在区间![]() 上可被
上可被![]() 替代;
替代;
②![]() 可被
可被![]() 替代的一个“替代区间”为
替代的一个“替代区间”为![]() ;
;
③![]() 在区间
在区间![]() 可被
可被![]() 替代,则
替代,则![]() ;
;
④![]() (
(![]() ),
),![]() (
(![]() ),则存在实数
),则存在实数![]() (
(![]() ),使得
),使得![]() 在区间
在区间![]() 上被
上被![]() 替代; 其中真命题有 .
替代; 其中真命题有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com