
已知双曲线C:![]() -
-![]() =1(0<
=1(0<![]() <1)的右焦点为B,过点B作直线交双曲线C的右支于M、N两点,试确定
<1)的右焦点为B,过点B作直线交双曲线C的右支于M、N两点,试确定![]() 的范围,使
的范围,使![]() ·
·![]() =0,其中点O为坐标原点.
=0,其中点O为坐标原点.
![]() ≤
≤![]() <
<![]() .
.
设M(x1,y1),N(x2,y2),由已知易求B(1,0),
①当MN垂直于x轴时,MN的方程为x=1,
设M(1,y0),N(1,-y0)(y0>0),
由![]() ·
·![]() =0,得y0=1,
=0,得y0=1,
∴M(1,1),N(1,-1).
又M(1,1),N(1,-1)在双曲线上,
∴![]() -
-![]() =1
=1![]()
![]() 2+
2+![]() -1=0
-1=0![]()
![]() =
=![]() , 4分
, 4分
因为0<![]() <1,所以
<1,所以![]() =
=![]() . 5分
. 5分
②当MN不垂直于x轴时,设MN的方程为y=k(x-1).
由 ,
,
得[![]() -(1-
-(1-![]() )k2]x2+2(1-
)k2]x2+2(1-![]() )k2x-(1-
)k2x-(1-![]() )(k2+
)(k2+![]() )=0, 8分
)=0, 8分
由题意知:![]() -(1-
-(1-![]() )k2≠0,
)k2≠0,
所以x1+x2=![]() ,
,
x1x2=![]() ,
,
于是y1y2=k2(x1-1)(x2-1)=![]() , 10分
, 10分
因为![]() ·
·![]() =0,且M、N在双曲线右支上,
=0,且M、N在双曲线右支上,
所以
![]()

?![]()

![]()
![]() <
<![]() <
<![]() . 13分
. 13分
由①②,知![]() ≤
≤![]() <
<![]() . 14分
. 14分


科目:高中数学 来源: 题型:
(2012年高考湖南卷理科5)已知双曲线C :![]() -
-![]() =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
A.![]() -
-![]() =1 B.
=1 B.![]() -
-![]() =1 C.
=1 C.![]() -
-![]() =1 D.
=1 D.![]() -
-![]() =1
=1
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西南宁二中高三(下)5月月考数学试卷(文科)(解析版) 题型:解答题
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为x=
,右准线方程为x=
查看答案和解析>>
科目:高中数学 来源:2014届湖南邵阳石齐学校高二第三次月考理科数学试卷(解析版) 题型:选择题
已知双曲线C :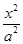 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
A.  -
-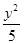 =1
B.
=1
B.  -
- =1 C.
=1 C.  -
- =1
D.
=1
D.  -
- =1
=1
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(湖南卷解析版) 题型:选择题
已知双曲线C : -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
A、 -
- =1 B、
=1 B、 -
- =1
C、
=1
C、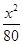 -
- =1
D、
=1
D、 -
- =1[w~#
=1[w~#
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com