
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益函数为R(x)= 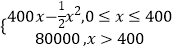 ,其中x是仪器的产量(单位:台);
,其中x是仪器的产量(单位:台);
(1)将利润f(x)表示为产量x的函数(利润=总收益﹣总成本);
(2)当产量x为多少台时,公司所获利润最大?最大利润是多少元?
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知两平行直线4x﹣2y+7=0,2x﹣y+1=0之间的距离等于坐标原点O到直线l:x﹣2y+m=0的距离的一半.
(1)求m的值;
(2)判断直线l与圆 ![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召![]() 名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成
名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成![]() 组第
组第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,已知第
,得到的频率分布直方图如图所示,已知第![]() 组有
组有![]() 人.
人.

(1)求该组织的人数;
(2)若在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参加某社区的宣传活动,应从第
名志愿者参加某社区的宣传活动,应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第![]() 组至少有
组至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .(x>0)
.(x>0)
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)若当x>0时,f(x)> ![]() 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
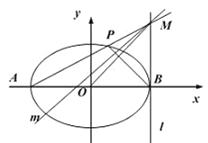
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的焦距为2,且过点
的焦距为2,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 分别是椭圆
分别是椭圆![]() 的左右顶点,直线
的左右顶点,直线![]() 经过点
经过点![]() 且垂直与轴,点
且垂直与轴,点![]() 是椭圆上异于
是椭圆上异于![]() 的任意一点,直线
的任意一点,直线![]() 交
交![]() 于点
于点![]() .
.
①设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值;
为定值;
②设过点![]() 垂直于
垂直于![]() 的直线为
的直线为![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为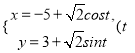 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 两点的极坐标和
两点的极坐标和![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问5分,(2)小问7分)
如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 过
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]()

(1)若![]() ,求椭圆的标准方程
,求椭圆的标准方程
(2)若![]() 求椭圆的离心率
求椭圆的离心率![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com