
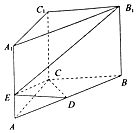
 如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).
如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).分析 (1)只需证明CD⊥平面ABB1A1即可得出结论;
(2)B1E⊥ED时,B1E⊥面CDE,此时,△AED∽△A1B1E,即可得出结论.
解答 证明:(1)∵AC=BC,点 D 为 AC 的中点,
∴CD⊥AB,
∵AA1⊥平面 ABC,CD?平面 ABC,
∴AA1⊥CD,
又AA1?平面ABB1A1,AB?平面ABB1A1,AA1∩AB=A,
∴CD⊥平面ABB1A1,
又B1E?平面ABB1A1,
∴CD⊥B1E.
(2)由题意,CD⊥平面A1B,B1E?平面A1B,∴B1E⊥CD,
B1E⊥ED时,B1E⊥面CDE,此时,△AED∽△A1B1E,
∴$\frac{{A}_{1}E}{2\sqrt{2}}=\frac{\sqrt{2}}{AE}$,∴A1E•AE=8,
∴4λ•(8-4λ)=8,
∴λ=1-$\frac{\sqrt{2}}{2}$.
点评 本题考查了线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-2x+5≥0 | B. | ?x∉R,x2-2x+5≤0 | C. | ?x∈R,x2-2x+5>0 | D. | ?x∉R,x2-2x+5>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{5}{3}$,5) | B. | (-$\frac{5}{3}$,0) | C. | [0,5] | D. | [-$\frac{5}{3}$,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-3)2+(y-1)2=9 | B. | (x+3)2+(y+1)2=9 | C. | ${({x-4})^2}+{({y-\frac{4}{3}})^2}=16$ | D. | (x-6)2+(y-2)2=9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4π+4 | B. | $4π+\frac{4}{3}$ | C. | 2π+4 | D. | $2π+\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com