
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 都是常数,
都是常数,![]() ,
,![]() .若
.若![]() 的零点为
的零点为![]() ,
,![]() ,则下列不等式正确的是( )
,则下列不等式正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
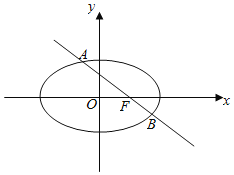
(1)求椭圆C的方程;
(2)如果直线l的斜率等于-1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用希腊字母![]() 表示,早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第七位的人,这比欧洲早了约1000年,在生活中,我们也可以通过设计下面的实验来估计
表示,早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第七位的人,这比欧洲早了约1000年,在生活中,我们也可以通过设计下面的实验来估计![]() 的值;从区间
的值;从区间![]() 内随机抽取200个数,构成100个数对
内随机抽取200个数,构成100个数对![]() ,其中满足不等式
,其中满足不等式![]() 的数对
的数对![]() 共有11个,则用随机模拟的方法得到的
共有11个,则用随机模拟的方法得到的![]() 的近似值为( )
的近似值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]()
![]() 的上顶点坐标为
的上顶点坐标为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)若椭圆上的点![]() 的横坐标为
的横坐标为![]() ,且位于第一象限,点
,且位于第一象限,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,
,![]() 是位于直线
是位于直线![]() 异侧的椭圆上的动点.
异侧的椭圆上的动点.
①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②若动点![]() 满足
满足![]() ,试探求直线
,试探求直线![]() 的斜率是否为定值?说明理由.
的斜率是否为定值?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点P(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心C的轨迹方程;
(2)过点(2,0)的直线l与动圆圆心C的轨迹交于A,B两点,求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com