
分析 先求出函数的零点,xn=-$\frac{(n+3)^3}{n^3}$-1,再求极限.
解答 解:令fn(x)=0得,
$(\frac{n+3}{n})^2$+$\frac{n}{n+3}$(x+1)=0,
解得xn=-$\frac{(n+3)^3}{n^3}$-1,其中,$\underset{lim}{n→∞}$$\frac{(n+3)^3}{n^3}$=1,
所以,$\underset{lim}{n→∞}$xn=-$\underset{lim}{n→∞}$$\frac{(n+3)^3}{n^3}$-1=-1-1=-2,
故填:-2.
点评 本题主要考查了极限及其运算,以及函数零点的求解,属于基础题.


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-1,0) | C. | (-2,-1) | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{x}$ | B. | y=ex | C. | y=-x2 | D. | y=lg|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | (3,+∞) | C. | $[2\sqrt{2},+∞)$ | D. | $(2\sqrt{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
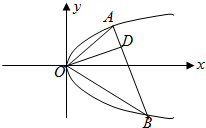 如图,已知直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).
如图,已知直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
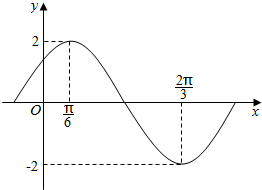 函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.
函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com