
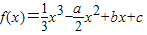 ,其中a>0,曲线y=f(x)在点P(0,f(0))处的切线方程为y=1.
,其中a>0,曲线y=f(x)在点P(0,f(0))处的切线方程为y=1.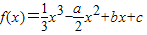 得:f(0)=c,f'(x)=x2-ax+b,f'(0)=b.由此能求出b和c.
得:f(0)=c,f'(x)=x2-ax+b,f'(0)=b.由此能求出b和c.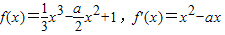 ,由于点(t,f(t))处的切线方程为y-f(t)=f'(t)(x-t),而点(0,2)在切线上,所以2-f(t)=f'(t)(-t),由此利用反证法能够证明f'(x1)≠f'(x2).
,由于点(t,f(t))处的切线方程为y-f(t)=f'(t)(x-t),而点(0,2)在切线上,所以2-f(t)=f'(t)(-t),由此利用反证法能够证明f'(x1)≠f'(x2).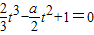 有三个相异的实根.由此能求出a的取值范围.
有三个相异的实根.由此能求出a的取值范围.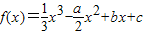 ,
,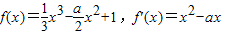 ,
,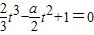 .
.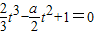 .
.
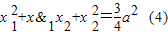
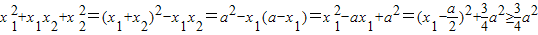 ,
, ,
,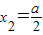 与x1≠x2矛盾,
与x1≠x2矛盾,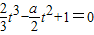 有三个相异的实根.
有三个相异的实根.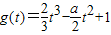 ,则
,则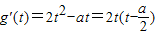 .
.| t | (-∞,0) | 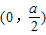 | 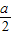 |  | |
| g'(t) | + | - | + | ||
| g(t) | ↗ | 极大值1 | ↘ | 极小值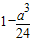 | ↗ |
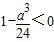 ,
,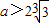 .
.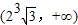


科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省株洲市醴陵二中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
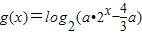 ,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.
,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省哈尔滨三中高三(上)9月月考数学试卷(文科)(解析版) 题型:解答题
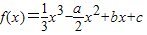 ,其中a>0,曲线y=f(x)在点P(0,f(0))处的切线方程为x轴
,其中a>0,曲线y=f(x)在点P(0,f(0))处的切线方程为x轴查看答案和解析>>
科目:高中数学 来源:2013年广东省高考数学模拟最后一卷(文科)(解析版) 题型:解答题
 处取得最大值2,其图象与轴的相邻两个交点的距离为
处取得最大值2,其图象与轴的相邻两个交点的距离为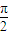 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com