
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a2=2,前n项和为 ![]() . (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
. (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
(II)设 ![]() ,数列{bn}的前n项和为Tn , 求使不等式
,数列{bn}的前n项和为Tn , 求使不等式 ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式x2﹣ax﹣2>0的解集为{x|x<﹣1或x>b}(b>﹣1).
(1)求a,b的值;
(2)当m>﹣ ![]() 时,解关于x的不等式(mx+a)(x﹣b)>0.
时,解关于x的不等式(mx+a)(x﹣b)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数fn(x)=xn+bx+c(n∈Z,b,c∈R).
(1)若n=﹣1,且f﹣1(1)=f﹣1( ![]() )=4,试求实数b,c的值;
)=4,试求实数b,c的值;
(2)设n=2,若对任意x1 , x2∈[﹣1,1]有|f2(x1)﹣f2(x2)|≤4恒成立,求b的取值范围;
(3)当n=1时,已知bx2+cx﹣a=0,设g(x)= ![]() ,是否存在正数a,使得对于区间
,是否存在正数a,使得对于区间 ![]() 上的任意三个实数m,n,p,都存在以f1(g(m)),f1(g(n)),f1(g(p))为边长的三角形?若存在,求出a的取值范围;若不存在,请说明理由.
上的任意三个实数m,n,p,都存在以f1(g(m)),f1(g(n)),f1(g(p))为边长的三角形?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间(﹣1,1)上的增函数f(x)= ![]() 为奇函数,且f(
为奇函数,且f( ![]() )=
)= ![]()
(1)求函数f(x)的解析式;
(2)解关于t的不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为零的等差数列,a10=15,且a3、a4、a7成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 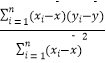 )=
)= 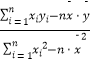 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com