
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为直角坐标原点,以极轴为
为直角坐标原点,以极轴为![]() 轴的正半轴建立平面直角坐标系
轴的正半轴建立平面直角坐标系![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的
个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的![]() ,纵坐标保持不变,得到曲线
,纵坐标保持不变,得到曲线![]()
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
科目:高中数学 来源: 题型:
【题目】2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X(40≤X<200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:
蔬菜量X | [40,80) | [80,120) | [120,160) | [160,200) |
天数 | 25 | 50 | 100 | 25 |
若将频率视为概率,试解答如下问题:
(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;
(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
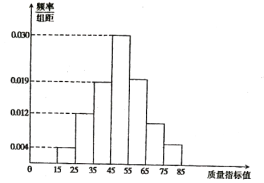
(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)用分层抽样的方法在区间![]() 内抽取一个容量为
内抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任意抽取
的样本,将该样本看成一个总体,从中任意抽取![]() 件桥梁构件,求这
件桥梁构件,求这![]() 件桥梁构件都在区间
件桥梁构件都在区间![]() 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人轮流吹同一只气球,当且仅当气球内的气体体积![]() (单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或
(单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或![]() ,且吹入的气体体积为整数.
,且吹入的气体体积为整数.
(1)若谁先吹破气球谁输,问谁有必胜策略?证明你的结论.
(2)若在不吹破气球的前提下,约定单次吹入的气体体积最大者为赢家(如果吹入的体积相同,则最先吹出最大体积者为赢家).问:谁有必胜策略?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】擎天柱为了防止魔方落入霸天虎手中,打算用激光刀将其销毁.擎天柱使用的方法是:每次切割可将魔方分成两个体积之比为![]() 的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有
的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有![]() 的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com