
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() .
.
(1)若![]() ,试判断
,试判断![]() 的奇偶性;
的奇偶性;
(2)若![]() ,
,![]() ,
,![]() ,证明
,证明![]() 的图像是轴对称图形,并求出对称轴.
的图像是轴对称图形,并求出对称轴.
【答案】(1)见解析(2)函数![]() 的图像是轴对称图形,其对称轴是直线
的图像是轴对称图形,其对称轴是直线![]() .
.
【解析】
(1)由![]() 得出
得出![]() ,于是得出
,于是得出![]() ,利用偶函数的定义得出
,利用偶函数的定义得出![]() ,利用奇函数的定义得出
,利用奇函数的定义得出![]() ,于是得出当
,于是得出当![]() 时,函数
时,函数![]() 为非奇非偶函数;
为非奇非偶函数;
(2)先得出![]() ,并设函数
,并设函数![]() 图象的对称轴为直线
图象的对称轴为直线![]() ,利用定义
,利用定义![]() ,列等式求出
,列等式求出![]() 的值,即可而出函数
的值,即可而出函数![]() 图象的对称轴方程.
图象的对称轴方程.
(1)由已知,![]() ,于是
,于是![]() ,则
,则![]() ,
,
若![]() 是偶函数,则
是偶函数,则![]() ,即
,即![]() ,
,
所以![]() 对任意实数
对任意实数![]() 恒成立,所以
恒成立,所以![]() .
.
若![]() 是奇函数,则
是奇函数,则![]() ,即
,即![]() ,
,
所以![]() 对任意实数
对任意实数![]() 恒成立,所以
恒成立,所以![]() .
.
综上,当![]() 时,
时,![]() 是偶函数;
是偶函数;
当![]() 时,
时,![]() 奇函数,当
奇函数,当![]() ,
,![]() 既不是奇函数也不是偶函数;
既不是奇函数也不是偶函数;
(2)![]() ,若函数
,若函数![]() 的图像是轴对称图形,且对称轴是直线
的图像是轴对称图形,且对称轴是直线![]() ,即对任意实数
,即对任意实数![]() ,
,![]() 恒成立,
恒成立,
![]() ,化简得
,化简得![]() ,
,
因为上式对任意![]() 成立,所以
成立,所以![]() ,
,![]() ,
,![]() .
.
所以,函数![]() 的图像是轴对称图形,其对称轴是直线
的图像是轴对称图形,其对称轴是直线![]() .
.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 15 | ||
女生 | 15 | ||
合计 |
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
(I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
(II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
参考公式: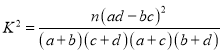 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可吸入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
某试点城市环保局从该市市区2015年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)

(1)求中位数.
(2)从这15天的数据中任取两天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列及数学期望.
(3)以这15天的PM2.5日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 由满足下列两个条件的数列
由满足下列两个条件的数列![]() 构成:①
构成:①![]() ②存在实数
②存在实数![]() 使得
使得![]() 对任意正整数
对任意正整数![]() 都成立.
都成立.
(1)现在给出只有5项的有限数列![]() 试判断数列
试判断数列![]() 是否为集合
是否为集合![]() 的元素;
的元素;
(2)设数列![]() 的前项和为
的前项和为![]() 且
且![]() 若对任意正整数
若对任意正整数![]() 点
点![]() 均在直线
均在直线![]() 上,证明:数列
上,证明:数列![]() 并写出实数
并写出实数![]() 的取值范围;
的取值范围;
(3)设数列![]() 若数列
若数列![]() 没有最大值,求证:数列
没有最大值,求证:数列![]() 一定是单调递增数列。
一定是单调递增数列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将两个数列的偏差距离定义为
,则将两个数列的偏差距离定义为![]() ,其中
,其中![]() .
.
(1)求数列1,2,7,8和数列2,3,5,6的偏差距离;
(2)设![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,
的集合,![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() ,若
,若![]() ,
,![]() ,
,![]() 和
和![]() 的偏差距离小于2020,求
的偏差距离小于2020,求![]() 最大值;
最大值;
(3)记![]() 是所有7项数列
是所有7项数列![]() 或
或![]() 的集合,
的集合,![]() ,且
,且![]() 中任何两个元素的偏差距离大于或等于3,证明:
中任何两个元素的偏差距离大于或等于3,证明:![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的右焦点分别为
的右焦点分别为![]() ,短袖长为
,短袖长为![]() ,点
,点![]() 在曲线
在曲线![]() 上,
上,![]() 直线
直线![]() 上,且
上,且![]() .
.
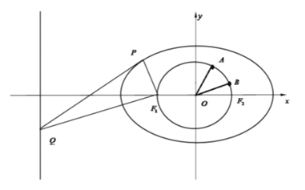
(1)求曲线的标准方程;
(2)试通过计算判断直线![]() 与曲线
与曲线![]() 公共点的个数.
公共点的个数.
(3)若点![]() 在都在以线段
在都在以线段![]() 为直径的圆上,且
为直径的圆上,且![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间几何体由两部分构成,上部是一个底面半径为1,高为2的圆锥,下部是一个底面半径为1,高为2的圆柱,圆锥和圆柱的轴在同一直线上,圆锥的下底面与圆柱的上底面重合,点![]() 是圆锥的顶点,
是圆锥的顶点,![]() 是圆柱下底面的一条直径,
是圆柱下底面的一条直径,![]() 、
、![]() 是圆柱的两条母线,
是圆柱的两条母线,![]() 是弧
是弧![]() 的中点.
的中点.
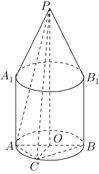
(1)求异面直线![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com