
【题目】已知函数f(x)=x﹣alnx﹣1, ![]() ,其中a为实数. (Ⅰ)求函数g(x)的极值;
,其中a为实数. (Ⅰ)求函数g(x)的极值;
(Ⅱ)设a<0,若对任意的x1、x2∈[3,4](x1≠x2), ![]() 恒成立,求实数a的最小值.
恒成立,求实数a的最小值.
【答案】解:(Ⅰ) ![]() ,令g'(x)=0,得x=1,列表如下:
,令g'(x)=0,得x=1,列表如下:
x | (﹣∞,1) | 1 | (1,+∞) |
g'(x) | + | 0 | ﹣ |
g(x) | ↗ | 极大值 | ↘ |
∴当x=1时,g(x)取得极大值g(1)=1,无极小值;…(4分)
(Ⅱ)当m=1时,a<0时,f(x)=x﹣alnx﹣1,x∈(0,+∞),
∵ ![]() 在[3,4]恒成立,∴f(x)在[3,4]上为增函数,
在[3,4]恒成立,∴f(x)在[3,4]上为增函数,
设 ![]() ,∵
,∵ ![]() 在[3,4]上恒成立,
在[3,4]上恒成立,
∴h(x)在[3,4]上为增函数,
不妨设x2>x1 , 则 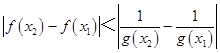 等价于:f(x2)﹣f(x1)<h(x2)﹣h(x1),即f(x2)﹣h(x2)<f(x1)﹣h(x1),
等价于:f(x2)﹣f(x1)<h(x2)﹣h(x1),即f(x2)﹣h(x2)<f(x1)﹣h(x1),
设 ![]() ,则u(x)在[3,4]上为减函数,
,则u(x)在[3,4]上为减函数,
∴ ![]() 在[3,4]上恒成立,
在[3,4]上恒成立,
∴ ![]() 恒成立,∴
恒成立,∴ 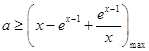 ,x∈[3,4],
,x∈[3,4],
设 ![]() ,∵
,∵ 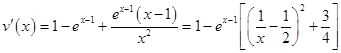 ,
,
∴ 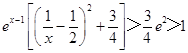 ,∴v'(x)>0,v(x)为减函数,
,∴v'(x)>0,v(x)为减函数,
∴v(x)在[3,4]上的最大值 ![]() ,∴
,∴ ![]() ,
,
∴a的最小值为 ![]()
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;(Ⅱ)设 ![]() ,根据函数的单调性得到h(x)在[3,4]上为增函数,问题等价于f(x2)﹣h(x2)<f(x1)﹣h(x1)设
,根据函数的单调性得到h(x)在[3,4]上为增函数,问题等价于f(x2)﹣h(x2)<f(x1)﹣h(x1)设 ![]() , 根据函数的单调性求出a的最小值即可.
, 根据函数的单调性求出a的最小值即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】如图程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”,执行该程序框图,若输入m,n分别为225、135,则输出的m=( ) 
A.5
B.9
C.45
D.90
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,把位于直线y=k与直线y=l(k、l均为常数,且k<l)之间的点所组成区域(含直线y=k,直线y=l)称为“k⊕l型带状区域”,设f(x)为二次函数,三点(﹣2,f(﹣2)+2)、(0,f(0)+2)、(2,f(2)+2)均位于“0⊕4型带状区域”,如果点(t,t+1)位于“﹣1⊕3型带状区域”,那么,函数y=|f(t)|的最大值为( )
A.![]()
B.3
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+λcosx的图像的一个对称中心是点( ![]() ,0),则函数g(x)=λsinxcosx+sin2x的图像的一条对称轴是直线( )
,0),则函数g(x)=λsinxcosx+sin2x的图像的一条对称轴是直线( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x=﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n∈N* , n≥3,k∈N* .
(1)求值: ①kCnk﹣nCn﹣1k﹣1;
② ![]() (k≥2);
(k≥2);
(2)化简:12Cn0+22Cn1+32Cn2+…+(k+1)2Cnk+…+(n+1)2Cnn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下: 
(Ⅰ)已知该校有400名学生,试估计全校学生中,每天学习不足4小时的人数;
(Ⅱ)若从学习时间不少于4小时的学生中选取4人,设选到的男生人数为X,求随机变量X的分布列;
(Ⅲ)试比较男生学习时间的方差 ![]() 与女生学习时间方差
与女生学习时间方差 ![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0 , y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1 , l2 , l1与l2相交于点M.
(Ⅰ)求p的值;
(Ⅱ)求动点M的轨迹方程.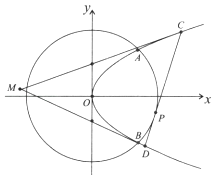
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com