
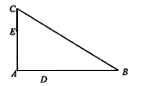
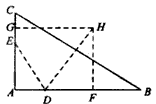
| (Ⅰ)证明:连接DE, 根据题意在△ADE和△ACB中,AD×AB=mn=AE×AC, 即 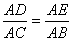 , ,又∠DAE=∠CAB,从而△ADE∽△ACB, 因此∠ADE=∠ACB, 所以C,B,D,E四点共圆。 (Ⅱ)解:m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12, 故AD=2,AB=12, 取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线, 两垂线相交于H点,连接DH, 因为C,B,D,E四点共圆, 所以C,B,D,E四点所在圆的圆心为H,半径为DH, 由于∠A=90°, 故GH∥AB,HF∥AC,HF=AG=5,DF= 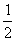 (12-2)=5, (12-2)=5,故C,B,D,E四点所在圆的半径为5 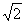 。 。 |
 |


科目:高中数学 来源: 题型:
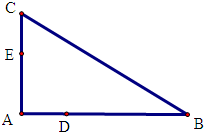 选修4-1:几何证明选讲
选修4-1:几何证明选讲查看答案和解析>>
科目:高中数学 来源: 题型:
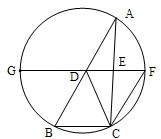 (2012•黑龙江)选修4-1:几何证明选讲
(2012•黑龙江)选修4-1:几何证明选讲查看答案和解析>>
科目:高中数学 来源:2013届甘肃省金昌市高二期中考试文科数学试卷(解析版) 题型:解答题
|
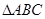 的边AB,AC上的点,且不与
的边AB,AC上的点,且不与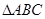 的顶点重合.已知AE的长的m,AC的长为n,AD,AB的长是关于x的方程
的顶点重合.已知AE的长的m,AC的长为n,AD,AB的长是关于x的方程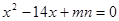 的两个根.
的两个根.

查看答案和解析>>
科目:高中数学 来源:2011年陕西省西安音乐学院高一上学期期末考试数学卷 题型:解答题
如图,D,E分别为三棱锥P—ABC的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC
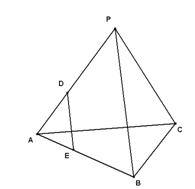
查看答案和解析>>
科目:高中数学 来源:2012届云南省高三上学期1月月考文科数学 题型:解答题
如图,D、E分别为△ABC的边AB、AC上的点,且不与△ABC的顶点重合。已知AE的长为 ,AC的长为
,AC的长为 ,AD、AB的长是关于
,AD、AB的长是关于 的方程
的方程 的两个根。
的两个根。
(I)证明:C、B、D、E四点共圆;
(II)若∠A=90°,且 ,求C、B、D、E所在圆的半径。
,求C、B、D、E所在圆的半径。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com