
【题目】已知正方体![]() .
.
求证:(ⅰ)面![]() 面
面![]() .
.
(ⅱ)![]() 面
面![]() .
.
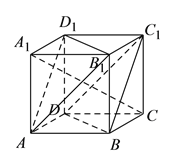
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)由平行四边形的性质可得![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ,同理可得
,同理可得![]() 平面
平面![]() ,从而根据面面平行的判定定理可得结论;(2)由三垂线定理得
,从而根据面面平行的判定定理可得结论;(2)由三垂线定理得![]() ,同理
,同理![]() ,在根据线面垂直的判定定理可得结论.
,在根据线面垂直的判定定理可得结论.
试题解析:( ![]() )由正方的性质可知
)由正方的性质可知![]() 且
且![]() ,
,
∴![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() .
.
∴平面![]() 平面
平面![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() 为
为![]() 在面
在面![]() 内的射影,
内的射影,
∵![]() ,
,
∴由三垂线定理得![]() ,
,
同理![]() ,
,
∴![]() 平面
平面![]() .
.
【方法点晴】本题主要考查正方体的性质、线面垂直的判定定理及面面垂直的判定定理,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.


科目:高中数学 来源: 题型:
【题目】给出下列几个命题:
① 命题![]() 任意
任意![]() ,都有
,都有![]() ,则
,则![]() 存在
存在![]() ,使得
,使得![]() .
.
② 命题“若![]() 且
且![]() ,则
,则![]() 且
且![]() ”的逆命题为假命题.
”的逆命题为假命题.
③ 空间任意一点![]() 和三点
和三点![]() ,则
,则![]() 是
是![]() 三点共线的充分不必要条件.
三点共线的充分不必要条件.
④ 线性回归方程![]() 对应的直线一定经过其样本数据点
对应的直线一定经过其样本数据点![]() 中的一个.
中的一个.
其中不正确的个数为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项的和Sn,点(n,Sn)在函数
的前n项的和Sn,点(n,Sn)在函数![]() =2x2+4x图象上:
=2x2+4x图象上:
(1)证明![]() 是等差数列;
是等差数列;
(2)若函数![]() ,数列{bn}满足bn=
,数列{bn}满足bn=![]() ,记cn=anbn,求数列
,记cn=anbn,求数列![]() 前n项和Tn;
前n项和Tn;
(3)是否存在实数λ,使得当x≤λ时,f(x)=﹣x2+4x﹣![]() ≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sin2x+2+2cos2x.
sin2x+2+2cos2x.
(1)求f(x)的最小正周期与单调递减区间;
(2)在△ABC中,a,b,c分别是角A、B、C的对边,若f(A)=4,b=1,△ABC的面积为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一期间,某商场决定从![]() 种服装、
种服装、![]() 种家电、
种家电、![]() 种日用品中,选出
种日用品中,选出![]() 种商品进行促销活动.
种商品进行促销活动.
(1)试求选出![]() 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高![]() 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有![]() 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为![]() 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为![]() 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为 ![]() 元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是![]() ,请问: 商场将奖金数额
,请问: 商场将奖金数额![]() 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程.
在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是 ![]() ,则sin2θ﹣cos2θ的值等于( )
,则sin2θ﹣cos2θ的值等于( ) 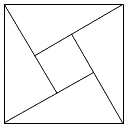
A.1
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com