
【题目】已知在△ABC中,角A,B,C的对边分别为a,b,c,且 ![]() +
+ ![]() =
= ![]() .
.
(1)求b的值;
(2)若cosB+ ![]() sinB=2,求a+c的取值范围.
sinB=2,求a+c的取值范围.
【答案】
(1)解:△ABC中, ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得b= ![]() ;
;
(2)解:∵cosB+ ![]() sinB=2,
sinB=2,
∴cosB=2﹣ ![]() sinB,
sinB,
∴sin2B+cos2B=sin2B+ ![]() =4sin2B﹣4
=4sin2B﹣4 ![]() sinB+4=1,
sinB+4=1,
∴4sin2B﹣4 ![]() sinB+3=0,
sinB+3=0,
解得sinB= ![]() ;
;
从而求得cosB= ![]() ,
,
∴B= ![]() ;
;
由正弦定理得 ![]() =
= ![]() =
= ![]() =
= ![]() =1,
=1,
∴a=sinA,c=sinC;
由A+B+C=π得A+C= ![]() ,
,
∴C= ![]() ﹣A,且0<A<
﹣A,且0<A< ![]() ;
;
∴a+c=sinA+sinC
=sinA+sin( ![]() ﹣A)
﹣A)
=sinA+sin ![]() cosA﹣cos
cosA﹣cos ![]() sinA
sinA
= ![]() sinA+
sinA+ ![]() cosA
cosA
= ![]() sin(A+
sin(A+ ![]() ),
),
∵0<A< ![]() ,∴
,∴ ![]() <A+
<A+ ![]() <
< ![]() ,
,
∴ ![]() <sin(A+
<sin(A+ ![]() )≤1,
)≤1,
∴ ![]() <
< ![]() sin(A+
sin(A+ ![]() )≤
)≤ ![]() ,
,
∴a+c的取值范围是( ![]() ,
, ![]() ].
].
【解析】(1)应用正弦、余弦定理化简 ![]() +
+ ![]() =
= ![]() ,即可求出b的值;(2)根据cosB+
,即可求出b的值;(2)根据cosB+ ![]() sinB=2与平方关系sin2B+cos2B=1,求得sinB、cosB,从而求得B的值,再由正弦定理求得a=sinA,c=sinC;利用A+B+C=π求得C=
sinB=2与平方关系sin2B+cos2B=1,求得sinB、cosB,从而求得B的值,再由正弦定理求得a=sinA,c=sinC;利用A+B+C=π求得C= ![]() ﹣A,且0<A<
﹣A,且0<A< ![]() ;
;
再利用三角恒等变换求a+c=sinA+sinC的取值范围.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】如图是函数 ![]() 图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() ,纵坐标不变
,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() ,纵坐标不变
,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆 ![]() 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的 ![]() 倍,得到曲线C.
倍,得到曲线C.
(1)求出C的普通方程;
(2)设直线l:x+2y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系, 求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(ω>0, ![]() )的部分图象如图所示,将函数f(x)的图象向右平移
)的部分图象如图所示,将函数f(x)的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若函数g(x)在区间
个单位后得到函数g(x)的图象,若函数g(x)在区间 ![]() (
( ![]() )上的值域为[﹣1,2],则θ= .
)上的值域为[﹣1,2],则θ= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S= ![]() .已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为 .
.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为 . 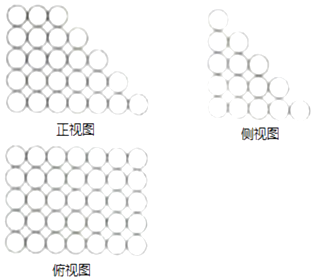
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(2,0),曲线C的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(Ⅱ)过点P且倾斜角为 ![]() 的直线l交曲线C于A,B两点,求|AB|.
的直线l交曲线C于A,B两点,求|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com