
已知 是定义在
是定义在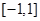 上的奇函数,且
上的奇函数,且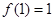 ,若
,若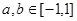 ,
,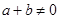 有
有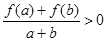 恒成立.
恒成立.
(1)判断 在
在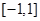 上是增函数还是减函数,并证明你的结论;
上是增函数还是减函数,并证明你的结论;
(2)若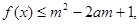 对所有
对所有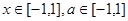 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(1)增函数,证明详见解析;(2) 或
或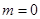 或
或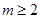
解析试题分析:(1)要判断函数的单调性一般可用增函数和减函数的定义或利用导函数判断,由于本题没有函数解析式,再结合题目特点,适于用定义判断,解决问题的关键是对照增函数和减函数的定义,再结合奇函数的条件,怎样通过适当的赋值构造出与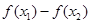 和
和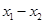 相关的式子,再判断符号解决,通过观察,只要令
相关的式子,再判断符号解决,通过观察,只要令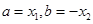 即可;(2)不等式恒成立问题一般要转化为函数的最值问题,先将原问题转化为
即可;(2)不等式恒成立问题一般要转化为函数的最值问题,先将原问题转化为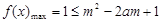 对任意
对任意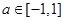 成立,再构造函数
成立,再构造函数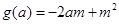 ,问题又转化为任意
,问题又转化为任意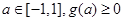 恒成立,此时可对
恒成立,此时可对 的系数
的系数 的符号讨论,但较为繁琐,较为简单的做法是只要
的符号讨论,但较为繁琐,较为简单的做法是只要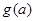 满足
满足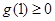 且
且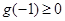 即可.
即可.
试题解析:(1)设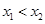 且
且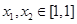 ,则
,则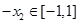 ,
,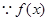 是奇函数
是奇函数 由题设知
由题设知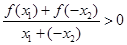 且
且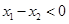 时
时 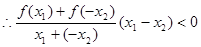 ,
,
即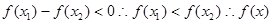 在
在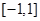 上是增函数
上是增函数
(2)由(1)知, 在
在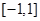 上是增函数,且
上是增函数,且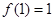
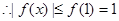
要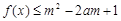 ,对所有
,对所有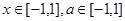 恒成立,需且只需
恒成立,需且只需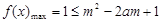 即
即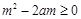 成立 ,
成立 ,
令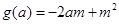 ,对任意
,对任意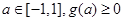 恒成立 需且只需
恒成立 需且只需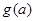 满足
满足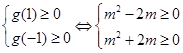 ,
,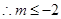 或
或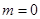 或
或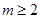
考点:函数的单调性、不等式恒成立.


科目:高中数学 来源: 题型:解答题
某连锁分店销售某种商品,每件商品的成本为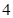 元,并且每件商品需向总店交
元,并且每件商品需向总店交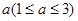 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为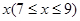 元时,一年的销售量为
元时,一年的销售量为 万件.
万件.
(Ⅰ)求该连锁分店一年的利润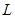 (万元)与每件商品的售价
(万元)与每件商品的售价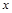 的函数关系式
的函数关系式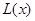 ;
;
(Ⅱ)当每件商品的售价为多少元时,该连锁分店一年的利润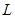 最大,并求出
最大,并求出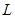 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近年来,网上购物已经成为人们消费的一种趋势。假设某淘宝店的一种装饰品每月的销售量y(单位:千件)与销售价格x(单位:元/件)满足关系式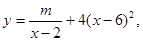 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)
(1)当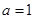 时,求
时,求 的单调区间;
的单调区间;
(2)若函数 在
在 上无零点,求
上无零点,求 的最小值;
的最小值;
(3)若对任意的 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com