
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为其焦点,
为其焦点,![]() 为其准线,过
为其准线,过![]() 任作一条直线交抛物线于
任作一条直线交抛物线于![]() 两点,
两点,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 在
在![]() 上的射影,
上的射影,![]() 为
为![]() 的中点,给出下列命题:
的中点,给出下列命题:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() 与
与![]() 的交点的
的交点的![]() 轴上;(5)
轴上;(5)![]() 与
与![]() 交于原点.
交于原点.
其中真命题的序号为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行围棋比赛,比赛要求双方下满五盘棋,开始时甲每盘棋赢的概率为![]() ,由于心态不稳,甲一旦输一盘棋,他随后每盘棋赢的概率就变为
,由于心态不稳,甲一旦输一盘棋,他随后每盘棋赢的概率就变为![]() .假设比赛没有和棋,且已知前两盘棋都是甲赢.
.假设比赛没有和棋,且已知前两盘棋都是甲赢.
(Ⅰ)求第四盘棋甲赢的概率;
(Ⅱ)求比赛结束时,甲恰好赢三盘棋的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,如图,C1,C2分别交x轴正半轴于点E,A.射线OD分别交C1,C2于点B,D,动点P满足直线BP与y轴垂直,直线DP与x轴垂直.
,如图,C1,C2分别交x轴正半轴于点E,A.射线OD分别交C1,C2于点B,D,动点P满足直线BP与y轴垂直,直线DP与x轴垂直.
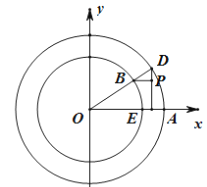
(1)求动点P的轨迹C的方程;
(2)过点E作直线l交曲线C与点M,N,射线OH⊥l与点H,且交曲线C于点Q.问:![]() 的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD-A1B1C1D1中,AB![]() CD,AB1⊥BC,且AA1=AB.求证:
CD,AB1⊥BC,且AA1=AB.求证:
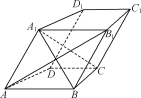
(1)AB![]() 平面D1DCC1;
平面D1DCC1;
(2)AB1⊥平面A1BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A.把![]() 上各点的横坐标变为原来的
上各点的横坐标变为原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B.把![]() 上各点的横坐标变为原来的
上各点的横坐标变为原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C.把![]() 向左平移
向左平移![]() 个单位长度,再把得到的曲线上各点的横坐标变为原来的
个单位长度,再把得到的曲线上各点的横坐标变为原来的![]() 倍.纵坐标不变,得到曲线
倍.纵坐标不变,得到曲线![]()
D.把![]() 向左平移
向左平移![]() 个单位长度,再把得到的曲线上各点的横坐标变为原来的
个单位长度,再把得到的曲线上各点的横坐标变为原来的![]() 倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com