
【题目】若函数f(x)= ![]() x+m在区间
x+m在区间 ![]() 上的最小值为3,求常数m的值及此函数当x∈[a,a+π](其中a可取任意实数)时的最大值.
上的最小值为3,求常数m的值及此函数当x∈[a,a+π](其中a可取任意实数)时的最大值.
【答案】解:函数f(x)= ![]() x+m=
x+m= ![]() sin2x+cos2x+m+1=2sin(2x+
sin2x+cos2x+m+1=2sin(2x+ ![]() )+m+1, 在区间
)+m+1, 在区间 ![]() 上,2x+
上,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],sin(2x+
],sin(2x+ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
2sin(2x+ ![]() )∈[﹣1,2],故函数的最小值为﹣1+m+1=3,求得m=3,
)∈[﹣1,2],故函数的最小值为﹣1+m+1=3,求得m=3,
此函数当x∈[a,a+π](其中a可取任意实数)时,由于函数y=2sin(2x+ ![]() )+4的周期为π,
)+4的周期为π,
故此函数的最大值为6
【解析】利用三角恒等变换化简函数的解析式,再利用正弦函数的定义域和值域,求得常数m的值及此函数当x∈[a,a+π](其中a可取任意实数)时的最大值.
【考点精析】掌握三角函数的最值是解答本题的根本,需要知道函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的首项a1=1,Sn是数列{an}的前n项和,且满足:anSn+1﹣an+1Sn+an﹣an+1= ![]() anan+1 , 则
anan+1 , 则 ![]() S12= .
S12= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg ![]() ,f(1)=0,且f(2)﹣f(
,f(1)=0,且f(2)﹣f( ![]() )=lg2.
)=lg2.
(1)求f(x)的表达式;
(2)若x∈(0,+∞)时方程f(x)=lgt有解,求实数t的取值范围;
(3)若函数y=f(x)﹣lg(8x+m)的无零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,底面
中,底面![]() 为正三角形,
为正三角形, ![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
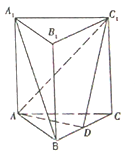
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得三棱锥
,使得三棱锥![]() 的体积是
的体积是![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知1丈为10尺,该锲体的三视图如图所示,则该锲体的体积为( )
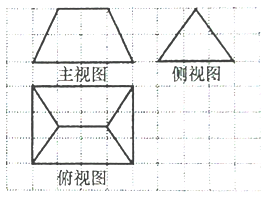
A. 10000立方尺 B. 11000立方尺 C. 12000立方尺 D. 13000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC. (Ⅰ)求A的大小;
(Ⅱ)求sinB+sinC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com