
【题目】已知平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数,r>0).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(θ为参数,r>0).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 ![]() ρsin(θ+
ρsin(θ+ ![]() )+1=0.
)+1=0.
(1)求圆C的圆心的极坐标;
(2)当圆C与直线l有公共点时,求r的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】一个总体中的100个个体的编号分别为0,1,2,3,…,99,依次将其分成10个小段,段号分别为0,1,2,…,9.现要用系统抽样的方法抽取一个容量为10的样本,规定如果在第0段随机抽取的号码为i,那么依次错位地取出后面各段的号码,即第k段中所抽取的号码的个位数为i+k或i+k-10(i+k≥10),则当i=7时,所抽取的第6个号码是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
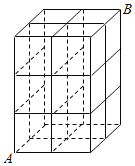
【题目】如图,某建筑工地搭建的脚手架局部类似于一个![]() 的长方体框架,一个建筑工人欲从
的长方体框架,一个建筑工人欲从![]() 处沿脚手架攀登至
处沿脚手架攀登至 ![]() 处,则其最近的行走路线中不连续向上攀登的概率为( )
处,则其最近的行走路线中不连续向上攀登的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P ABCD中,E是棱PC上一点,且2![]() ,底面ABCD是边长为2的正方形,△PAD为正三角形,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l,且平面PAD⊥平面ABCD.
,底面ABCD是边长为2的正方形,△PAD为正三角形,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l,且平面PAD⊥平面ABCD.

(1)求证:l∥EF;
(2)求四棱锥P-ABEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() ,
, ![]() ,
,![]()
![]() ,且
,且![]() 两两垂直.给出下列四个命题:
两两垂直.给出下列四个命题:

①三棱锥![]() 的体积为定值;
的体积为定值;
②经过![]() 四点的球的直径为
四点的球的直径为![]() ;
;
③直线![]() ∥平面
∥平面![]() ;
;
④直线![]() 所成的角为
所成的角为![]() ;
;
其中真命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的四棱锥S﹣ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E为线段BS上的一个动点. 
(1)证明:DE和SC不可能垂直;
(2)当点E为线段BS的三等分点(靠近B)时,求二面角S﹣CD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位招聘面试,每次从试题库随机调用一道试题,若调用的是A类型试题,则使用后该试题回库,并增补一道A类试题和一道B类型试题入库,此次调题工作结束;若调用的是B类型试题,则使用后该试题回库,此次调题工作结束.试题库中现共有n+m道试题,其中有n道A类型试题和m道B类型试题,以X表示两次调题工作完成后,试题库中A类试题的数量.
(Ⅰ)求X=n+2的概率;
(Ⅱ)设m=n,求X的分布列和均值(数学期望)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(1,2,3),B(2,1,2),C(1,1,2),O为坐标原点,点D在直线OC上运动,则当![]() ·
·![]() 取最小值时,点D的坐标为( )
取最小值时,点D的坐标为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com