
【题目】已知平面![]() 平面ABC,P、P在平面ABC的同侧,二面角
平面ABC,P、P在平面ABC的同侧,二面角![]() 的平面角为钝角,Q到平面ABC的距离为
的平面角为钝角,Q到平面ABC的距离为![]() ,
,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() ,
,![]() .
.
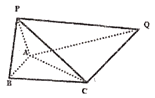
(1)求证:面![]() 平面PAB;
平面PAB;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】某学校随机抽取部分学生调查其上学路上所需时间(单位:分钟),并将所得数据制成频率分布直方图(如图),若上学路上所需时间的范围为![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中a的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,若招收学生1200人,请估计所招学生中有多少人可以申请住宿;
(3)求该校学生上学路上所需的平均时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若同时满足下列条件:
,若同时满足下列条件:
①![]() 在
在![]() 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ;
;
那么把![]() 叫闭函数.
叫闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( )
①对于命题![]() ,使得
,使得![]() ,则
,则![]() ,均有
,均有![]() ;
;
②命题“已知x,![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是真命题;
”是真命题;
③设![]() ,
,![]() 是非零向量,则“
是非零向量,则“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
④![]() 是直线
是直线![]() 与直线
与直线![]() 互相垂直的充要条件.
互相垂直的充要条件.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,
,![]() 成等差数列,其公差为
成等差数列,其公差为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,证明
,证明![]() 成等比数列(
成等比数列(![]() );
);
(3)若对任意![]() ,
,![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,设
,设![]() ,证明数列
,证明数列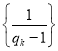 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B分别为双曲线![]() (a>0,b>0)的左、右顶点,双曲线的实轴长为4
(a>0,b>0)的左、右顶点,双曲线的实轴长为4![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求双曲线的方程;
(2)已知直线y=![]() x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使
x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使![]() ,求t的值及点D的坐标.
,求t的值及点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着教育信息化2.0时代的到来,依托网络进行线上培训越来越便捷,逐步成为实现全民终身学习的重要支撑.最近某高校继续教育学院采用线上和线下相结合的方式开展了一次300名学员参加的“国学经典诵读”专题培训.为了解参训学员对于线上培训、线下培训的满意程度,学院随机选取了50名学员,将他们分成两组,每组25人,分别对线上、线下两种培训进行满意度测评,根据学员的评分(满分100分)绘制了如下茎叶图:
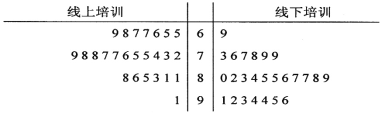
(1)根据茎叶图判断学员对于线上、线下哪种培训的满意度更高?并说明理由;
(2)求50名学员满意度评分的中位数![]() ,并将评分不超过
,并将评分不超过![]() 、超过
、超过![]() 分别视为“基本满意”、“非常满意”两个等级.
分别视为“基本满意”、“非常满意”两个等级.
(i)利用样本估计总体的思想,估算本次培训共有多少学员对线上培训非常满意?
(ii)根据茎叶图填写下面的列联表:
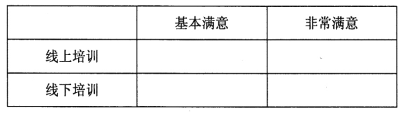
并根据列联表判断能否有99.5%的把握认为学员对两种培训方式的满意度有差异?
附: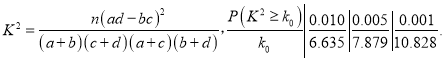
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com