
已知a>0,函数f(x)=-2asin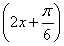 +2a+b,当x∈
+2a+b,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1)求常数a、b的值;
(2)设g(x)=f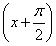 且lgg(x)>0,求g(x)的单调区间.
且lgg(x)>0,求g(x)的单调区间.
(1)a=2,b=-5.(2)单调增区间为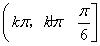 (k∈Z),单调减区间为
(k∈Z),单调减区间为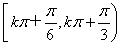 (k∈Z)
(k∈Z)
【解析】(1)∵x∈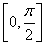 ,∴2x+
,∴2x+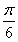 ∈
∈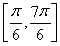 .∴sin
.∴sin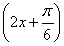 ∈
∈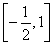 ,
,
∴-2asin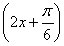 ∈[-2a,a],∴f(x)∈[b,3a+b].
∈[-2a,a],∴f(x)∈[b,3a+b].
又∵-5≤f(x)≤1,∴b=-5,3a+b=1,因此a=2,b=-5.
(2)由(1)知a=2,b=-5,∴f(x)=-4sin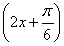 -1,
-1,
g(x)=f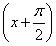 =-4sin
=-4sin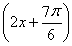 -1=4sin
-1=4sin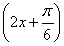 -1.
-1.
又由lgg(x)>0,得g(x)>1,∴4sin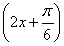 -1>1,∴sin
-1>1,∴sin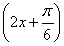 >
>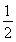 ,
,
∴2kπ+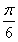 <2x+
<2x+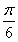 <2kπ+
<2kπ+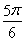 ,k∈Z.
,k∈Z.
由2kπ+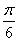 <2x+
<2x+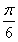 ≤2kπ+
≤2kπ+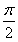 (k∈Z),得g(x)的单调增区间为
(k∈Z),得g(x)的单调增区间为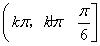 (k∈Z).
(k∈Z).
由2kπ+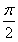 ≤2x+
≤2x+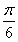 <2kπ+
<2kπ+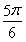 ,得g(x)的单调减区间为
,得g(x)的单调减区间为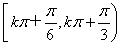 (k∈Z)
(k∈Z)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第7课时练习卷(解析版) 题型:解答题
在△ABC中,角A、B、C所对的边分别是a、b、c,已知c=2,C=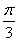 .
.
(1)若△ABC的面积等于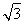 ,求a、b;
,求a、b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第4课时练习卷(解析版) 题型:解答题
已知α、β∈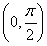 ,sinα=
,sinα=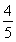 ,tan(α-β)=-
,tan(α-β)=-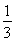 ,求cosβ的值.
,求cosβ的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第3课时练习卷(解析版) 题型:填空题
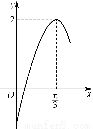
若函数f(x)=Asin(2x+φ)(A>0,-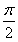 <φ<
<φ<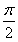 )的部分图象如图所示,则f(0)=________.
)的部分图象如图所示,则f(0)=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第3课时练习卷(解析版) 题型:解答题
为了得到函数y=2sin (x∈R)的图象,只需把函数y=2sinx(x∈R)的图象上所有的点经过怎样的变换得到?
(x∈R)的图象,只需把函数y=2sinx(x∈R)的图象上所有的点经过怎样的变换得到?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第3课时练习卷(解析版) 题型:填空题
用数学归纳法证明不等式“2n>n2+1对于n≥n0的自然数n都成立”时,第一步证明中的起始值n0应取为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com