
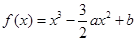 ,
,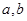 为实数,
为实数,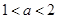 .
. 在区间
在区间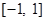 上的最小值、最大值分别为
上的最小值、最大值分别为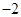 、1,求
、1,求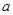 、
、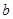 的值;
的值;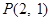 且与曲线
且与曲线 相切的直线
相切的直线 的方程;
的方程;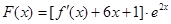 ,试判断函数
,试判断函数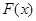 的极值点个数.
的极值点个数.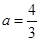 ,
,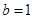 为所求. (Ⅱ)
为所求. (Ⅱ)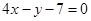 或
或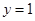 .
. 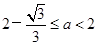 时,
时,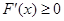 ,函数
,函数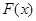 为单调递增,极值点个数为0;
为单调递增,极值点个数为0;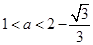 时,此时方程
时,此时方程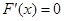 有两个不相等的实数根,根据极值点的定义,
有两个不相等的实数根,根据极值点的定义,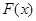 有两个极值点.
有两个极值点.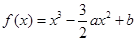 ,
,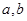 为实数,
为实数,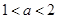 .求解导数。判定单调性和最值,结合
.求解导数。判定单调性和最值,结合 在区间
在区间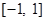 上的最小值、最大值分别为
上的最小值、最大值分别为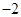 、1得到参数
、1得到参数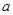 、
、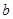 的值;
的值;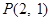 且与曲线
且与曲线 相切的直线
相切的直线 的方程;
的方程;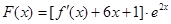 ,函数
,函数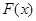 的极值点个数就是分析单调性来得到结论。
的极值点个数就是分析单调性来得到结论。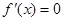 ,得
,得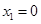 ,
,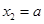 .
.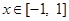 ,
,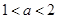 ,
,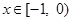 时,
时,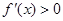 ,
, 递增;
递增;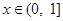 时,
时,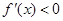 ,
, 递减.
递减. 在区间
在区间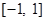 上的最大值为
上的最大值为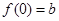 ,∴
,∴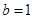 .……………………2分
.……………………2分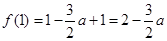 ,
,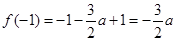 ,∴
,∴ 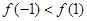 .
.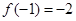 ,即
,即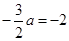 ,得
,得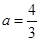 .
. 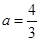 ,
,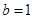 为所求. ………………………………4分
为所求. ………………………………4分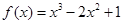 ,
,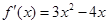 ,点
,点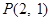 在曲线
在曲线 上.
上.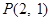 时,切线
时,切线 的斜率
的斜率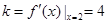 ,
, 的方程为
的方程为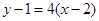 ,即
,即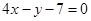 . ……………………5分
. ……………………5分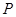 不是切点时,设切点为
不是切点时,设切点为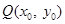
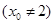 ,
, 的斜率
的斜率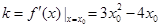 ,
, 的方程为
的方程为 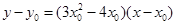 .
.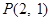 在
在 上,∴
上,∴ 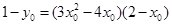 ,
,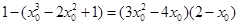 ,
,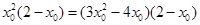 ,
,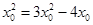 ,即
,即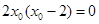 ,∴
,∴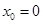 .
. 的方程为
的方程为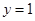
 的方程为
的方程为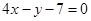 或
或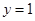 . ………………………………8分
. ………………………………8分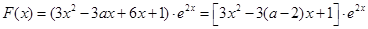 .
.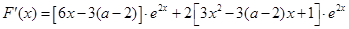
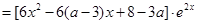
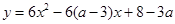 的判别式为
的判别式为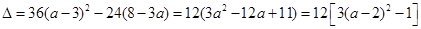 ,
,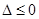 ,得:
,得: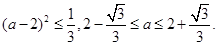
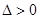 ,得
,得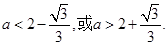 ………………………………10分
………………………………10分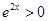 ,
,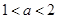 ,
,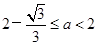 时,
时,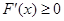 ,函数
,函数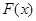 为单调递增,极值点个数为0;
为单调递增,极值点个数为0;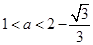 时,此时方程
时,此时方程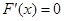 有两个不相等的实数根,根据极值点的定义,
有两个不相等的实数根,根据极值点的定义,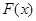 有两个极值点. ………………………………12分
有两个极值点. ………………………………12分

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源:不详 题型:解答题
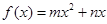 ,函数
,函数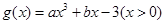 ,且有
,且有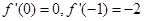 ,
,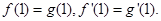
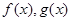 的解析式;
的解析式;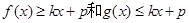 成立,若存在,求出k和p的值;若不存在,说明理由.
成立,若存在,求出k和p的值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
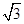 )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )A.[0,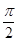 ) ) | B.[0,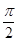 )∪[ )∪[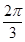 , ,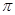 ) ) |
C.[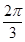 , ,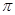 ) ) | D.[0,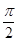 )∪( )∪(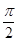 , ,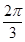 ] ] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com