
【题目】第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议(简称两会)将分别于![]() 年
年![]() 月
月![]() 日和
日和![]() 月
月![]() 日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占
日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占![]() .现从参与者中随机选出
.现从参与者中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第
人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
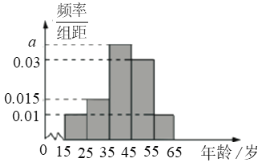
(Ⅰ)现在要从年龄较小的第![]() ,
,![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送礼品,求抽取的
人赠送礼品,求抽取的![]() 人中至少有
人中至少有![]() 人年龄在第
人年龄在第![]() 组的概率;
组的概率;
(Ⅱ)把年龄在第![]() ,
,![]() ,
,![]() 组的人称为青少年组,年龄在第
组的人称为青少年组,年龄在第![]() ,
,![]() 组的人称为中老年组,若选出的
组的人称为中老年组,若选出的![]() 人中不关注网约车安全问题的人中老年人有
人中不关注网约车安全问题的人中老年人有![]() 人,问是否有
人,问是否有![]() 的把握认为是否关注网约车安全问题与年龄有关?附:
的把握认为是否关注网约车安全问题与年龄有关?附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
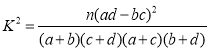 ,
,![]()
【答案】(Ⅰ)![]() ;(Ⅱ)没有
;(Ⅱ)没有![]() 的把握认为是否关注网约车安全问题与年龄有关.
的把握认为是否关注网约车安全问题与年龄有关.
【解析】
(Ⅰ)按第1组和第2组的人数,求出抽取5人中从第1组和第2组分别抽取的人数,并按组对抽出的5人进行编号,列出从5人中抽取2人的所有情况,确定2人都在第2组的方法个数,按古典概型概率公式和对立事件的概率关系,即可求解;
(Ⅱ)不关注网约车安全问题的人中老年人有![]() 人,则青年人有
人,则青年人有![]() 人,列出列联表,根据公式求出
人,列出列联表,根据公式求出![]() 的观测值,即可求出结论.
的观测值,即可求出结论.
(Ⅰ)由频率直方图可得第1组和第2组的频率分别为![]() ,
,
所以第![]() ,
,![]() 组的人数分别为
组的人数分别为![]() ,
,![]() ,
,
从第![]() ,
,![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,
人,
则第![]() ,
,![]() 组抽取的人数分别为
组抽取的人数分别为![]() ,
,![]() .
.
抽取的第![]() ,
,![]() 组中
组中![]() 人记为
人记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所有可能情况为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
全部都在第![]() 组的情况有:
组的情况有:![]() ,
,![]() ,
,![]() ,
,
记从![]() 人中随机抽取
人中随机抽取![]() 人,至少有
人,至少有![]() 人年龄在第
人年龄在第![]() 组为事件
组为事件![]() ,
,
则![]() .
.
(Ⅱ)由题意得![]() 列联表如下:
列联表如下:
关注网约车安全 | 不关注网约车安全 | 合计 | |
青少年 |
|
|
|
中老年 |
|
|
|
合计 |
|
|
|
![]()
所以没有![]() 的把握认为是否关注网约车安全问题与年龄有关.
的把握认为是否关注网约车安全问题与年龄有关.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为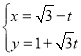 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三陵锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点.
的中点.
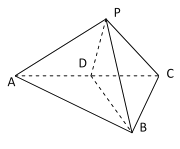
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角为锐角,且棱锥
的平面角为锐角,且棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() ,(t为参数),曲线
,(t为参数),曲线![]() :
:![]() ,(
,(![]() 为参数).
为参数).
(1)以原点为极点,x轴正半轴为极轴建立极坐标系;当![]() 时,求
时,求![]() 与
与![]() 的交点的极坐标(其中极径
的交点的极坐标(其中极径![]() ,极角
,极角![]() );
);
(2)过坐标原点O作![]() 的垂线,垂足为A,P为OA中点,当
的垂线,垂足为A,P为OA中点,当![]() 变化时,求P点轨迹的参数方程,并指出它是什么曲线.
变化时,求P点轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com