
分析 (1)设Ai:第i个路口遇到红灯(i=1,2,3),最多遇到1次红灯为A事件,由$P(A)=P(\overline{A_1}\overline{A_2}\overline{A_3})+P({A_1}\overline{A_2}\overline{A_3})+P(\overline{A_1}{A_2}\overline{A_3})+P(\overline{A_1}\overline{A_2}{A_3})$,能求出最多遇到1次红灯的概率.
(2)依题意,X的可能取值为0,1,2,3.分别求出相应的概率,由此能求出随机变量X的分布列和EX.
解答 解:(1)设Ai:第i个路口遇到红灯(i=1,2,3)
最多遇到1次红灯为A事件,
则$P(A)=P(\overline{A_1}\overline{A_2}\overline{A_3})+P({A_1}\overline{A_2}\overline{A_3})+P(\overline{A_1}{A_2}\overline{A_3})+P(\overline{A_1}\overline{A_2}{A_3})$
=(1-$\frac{3}{4}$)(1-$\frac{4}{5}$)(1-$\frac{1}{2}$)+$\frac{3}{4}(1-\frac{4}{5})(1-\frac{1}{2})$+(1-$\frac{3}{4}$)×$\frac{4}{5}×(1-\frac{1}{2})$+$(1-\frac{3}{4})(1-\frac{4}{5})×\frac{1}{2}$=$\frac{9}{40}$.
(2)依题意,X的可能取值为0,1,2,3.
$P(X=0)=P(\overline{A_1}\overline{A_2}\overline{A_3})=\frac{1}{40}$,
$P(X=1)=P({A_1}\overline{A_2}\overline{A_3})+P(\overline{A_1}{A_2}\overline{A_3})+P(\overline{A_1}\overline{A_2}{A_3})=\frac{1}{5}$,
$P(X=2)=P({A_1}{A_2}\overline{A_3})+P({A_1}\overline{A_2}{A_3})+P(\overline{A_1}{A_2}{A_3})=\frac{19}{40}$,
$P(X=3)=P({A_1}{A_2}{A_3})=\frac{3}{10}$,
随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{40}$ | $\frac{1}{5}$ | $\frac{19}{40}$ | $\frac{3}{10}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意对立事件概率公式、相互独立事件概率乘法公式和互斥事件概率加法公式的合理运用.


科目:高中数学 来源: 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
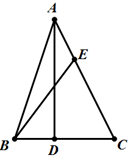 如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6
如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com