
【题目】如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ![]() ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.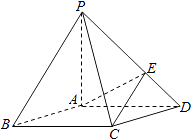
(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
【答案】解:(Ⅰ)证明因为底面ABCD是菱形,∠ABC=60°,
所以AB=AD=AC=a,在△PAB中,
由PA2+AB2=2a2=PB2知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
(Ⅱ)解:作EG∥PA交AD于G,
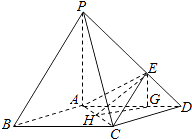
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连接EH,
则EH⊥AC,∠EHG即为二面角θ的平面角.
又PE:ED=2:1,所以 ![]() .
.
从而 ![]() ,θ=30°.
,θ=30°.
(Ⅲ)解法一以A为坐标原点,直线AD、AP分别为y轴、z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系如图.

由题设条件,相关各点的坐标分别为 ![]() .
. ![]() .
.
所以 ![]() .
. ![]() .
. ![]() .
.
设点F是棱PC上的点, ![]() ,其中0<λ<1,
,其中0<λ<1,
则 ![]() =
= ![]() .
.
令 ![]() 得
得  即
即 
解得 ![]() .即
.即 ![]() 时,
时, ![]() .
.
亦即,F是PC的中点时, ![]() 、
、 ![]() 、
、 ![]() 共面.
共面.
又BF平面AEC,所以当F是棱PC的中点时,BF∥平面AEC.
解法二:当F是棱PC的中点时,BF∥平面AEC,证明如下,
证法一:取PE的中点M,连接FM,则FM∥CE.①
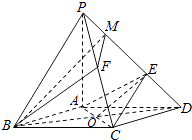
由 ![]() ,知E是MD的中点.
,知E是MD的中点.
连接BM、BD,设BD∩AC=O,则O为BD的中点.
所以BM∥OE.②
由①、②知,平面BFM∥平面AEC.
又BF平面BFM,所以BF∥平面AEC.
证法二:
因为 ![]() =
= ![]() =
= ![]() .
.
所以 ![]() 、
、 ![]() 、
、 ![]() 共面.
共面.
又BF平面ABC,从而BF∥平面AEC.
【解析】(I)利用勾股定理可证PA⊥AB、PA⊥AD,进而可证PA⊥平面ABCD;(II)先找出以AC为棱,EAC与DAC为面的二面角θ的平面角,再利用解三角形可得以AC为棱,EAC与DAC为面的二面角θ的大小;(III)解法一:先建立空间直角坐标系,再证![]() 、
、![]() 、
、![]() 共面,进而可得点F的位置;解法二:证法一先利用三角形的中位线可证BM∥OE,再利用面面平行可证BF∥平面AEC;证法二利用向量表示可证
共面,进而可得点F的位置;解法二:证法一先利用三角形的中位线可证BM∥OE,再利用面面平行可证BF∥平面AEC;证法二利用向量表示可证![]() 、
、![]() 、
、![]() 共面,进而可证BF∥平面AEC.
共面,进而可证BF∥平面AEC.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 上的一个最高点的坐标为
上的一个最高点的坐标为![]() ,由此点到相邻最低点间的曲线与x轴交于点
,由此点到相邻最低点间的曲线与x轴交于点![]() ,若
,若![]() .
.
(1)求![]() 的解析式.
的解析式.
(2)求![]() 在
在![]() 上的值域.
上的值域.
(3)若对任意实数![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(t)是某港口水的深度y(米)关于时间t(小时)的函数,其中![]() .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 12 | 14.9 | 11.9 | 9 | 12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数![]() 的图象.⑴求
的图象.⑴求![]() 的解析式;⑵设水深不小于
的解析式;⑵设水深不小于![]() 米时,轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事,然后再出港。问该轮船最多能在港口停靠多长时间?
米时,轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事,然后再出港。问该轮船最多能在港口停靠多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=5,PD=8,点E,F分别是PB,DC的中点.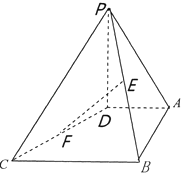
(1)求证:EF∥平面PAD;
(2)求EF与平面PDB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},a1=2,a2=6,且满足![]() =2(n≥2且n∈N+)
=2(n≥2且n∈N+)
(1)证明:新数列{an+1-an}是等差数列,并求出an的通项公式
(2)令bn=![]() ,设数列{bn}的前n项和为Sn,证明:S2n-Sn<5
,设数列{bn}的前n项和为Sn,证明:S2n-Sn<5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+3x2+1,若至少存在两个实数m,使得f(﹣m),f(1)、f(m+2)成等差数列,则过坐标原点作曲线y=f(x)的切线可以作( )
A.3条
B.2条
C.1条
D.0条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() ,a∈R.
,a∈R.
(1)若f(x)的最小值为0,求实数a的值;
(2)证明:当a=2时,不等式f(x)≥ ![]() ﹣e1﹣x恒成立.
﹣e1﹣x恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人独立地对某一技术难题进行攻关.甲能攻克的概率为 ![]() ,乙能攻克的概率为
,乙能攻克的概率为 ![]() ,丙能攻克的概率为
,丙能攻克的概率为 ![]() .
.
(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励a万元.奖励规则如下:若只有1人攻克,则此人获得全部奖金a万元;若只有2人攻克,则奖金奖给此二人,每人各得 ![]() 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得 ![]() 万元.设甲得到的奖金数为X,求X的分布列和数学期望.
万元.设甲得到的奖金数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com