
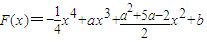 .(a,b为常数)
.(a,b为常数) ,F(4)=32+b,F(0)=b
,F(4)=32+b,F(0)=b
 =0必有两根,且其一根为0故
=0必有两根,且其一根为0故 =0仅有一根
=0仅有一根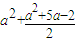 =0,即3a2+5a-2=0解得a=-2或a=
=0,即3a2+5a-2=0解得a=-2或a= 代入①验证知,a=-2或a=
代入①验证知,a=-2或a= 符合题意
符合题意 时,能使函数F(x)在x1(或者x2)处取得的极值为b
时,能使函数F(x)在x1(或者x2)处取得的极值为b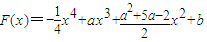 在[-2,2]上的最小值为F(2)=-4+8a+2a2+10a-4+b
在[-2,2]上的最小值为F(2)=-4+8a+2a2+10a-4+b

 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
(09年济宁质检文)(14分)
已知函数![]() 和
和![]() (a,b为常数)的图像在
(a,b为常数)的图像在![]() 处有公切线
处有公切线
(1)求实数a的值;
(2)求函数![]() 的极大值和极小值;
的极大值和极小值;
(3)关于x的方程![]() 有几个不同的实数解?
有几个不同的实数解?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省实验中学、华师附中、广雅中学、深圳中学四校联考高三(上)期末数学试卷(文科)(解析版) 题型:解答题
 ,其中a,b为常数.
,其中a,b为常数.查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三上学期期末考试理科数学 题型:解答题
(本小题满分13分)
已知函数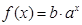 (其中a,b为常数且
(其中a,b为常数且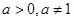 )的反函数的图象经过点A(4,1)和B(16,3)。
)的反函数的图象经过点A(4,1)和B(16,3)。
(1)求a,b的值;
(2)若不等式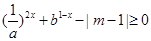 在
在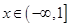 上恒成立,求实数m的取值范围。
上恒成立,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第一次月考理科数学试卷 题型:解答题
(本小题13分)已知函数 ,实数a,b为常数),
,实数a,b为常数),
(Ⅰ)若a=1, 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;
(Ⅱ)若a≥2,b=1,判断方程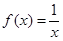 在(0,1]上解的个数。
在(0,1]上解的个数。
查看答案和解析>>
科目:高中数学 来源:2010年江西省高三热身卷数学(理)试题 题型:解答题
(本题14分)
已知函数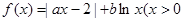 ,实数a,b为常数),
,实数a,b为常数),
(1)若a=1,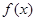 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程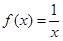 在(0,1]上解的个数。
在(0,1]上解的个数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com