【题目】已知函数
（
，
是实数常数）的图像上的一个最高点是
，与该最高点最近的一个最低点是
.
（1）求函数
的解析式及其单调递增区间；
（2）在
中，角
所对的边分别为
，且
，角
的取值范围是区间
。当
时，试求函数的取值范围。
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，直线
的参数方程为
（
为参数），以原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
（Ⅰ）求曲线的直角坐标方程，并指出其表示何种曲线；（Ⅱ）设直线与曲线交于
两点，若点
的直角坐标为
，试求当
时，
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
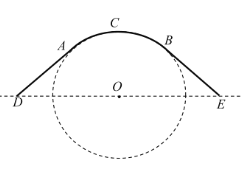
【题目】某公园为了美化环境和方便顾客，计划建造一座圆弧形拱桥，已知该桥的剖面如图所示，共包括圆弧形桥面
和两条长度相等的直线型路面
、
，桥面跨度
的长不超过
米，拱桥所在圆的半径为
米，圆心
在水面上，且和所在直线与圆分别在连结点
和
处相切.设
，已知直线型桥面每米修建费用是
元，弧形桥面每米修建费用是
元.
（1）若桥面（线段、和弧）的修建总费用为
元，求关于
的函数关系式；
（2）当为何值时，桥面修建总费用最低？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）若曲线
在
处的切线的方程为
，求实数
的值；
（2）设
，若对任意两个不等的正数
，都有
恒成立，求实数的取值范围；
（3）若在
上存在一点
，使得
成立，求实数的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的左、右焦点分别为
， 
，且离心率为
， 
为椭圆上任意一点，当
时， 
的面积为1.
（1）求椭圆
的方程；
（2）已知点
是椭圆
上异于椭圆顶点的一点，延长直线
， 
分别与椭圆交于点
， 
，设直线
的斜率为
，直线
的斜率为
，求证： 
为定值.
【答案】（1）
；（2）
【解析】试题分析：（1）设
由题
，由此求出
,可得椭圆
的方程；
（2）设
， 
，
当直线
的斜率不存在时，可得
；
当直线
的斜率不存在时，同理可得
.
当直线
、
的斜率存在时，
，
设直线
的方程为
，则由
消去
通过运算可得
，同理可得
，由此得到直线
的斜率为
，
直线
的斜率为
，进而可得
.
试题解析：（1）设由题
，
解得
，则
，
椭圆
的方程为
.
（2）设
， 
，
当直线
的斜率不存在时，设
，则
，
直线
的方程为
代入
，可得
，
， 
，则
，
直线
的斜率为
，直线
的斜率为
，
，
当直线
的斜率不存在时，同理可得
.
当直线
、
的斜率存在时，，
设直线
的方程为
，则由
消去
可得：
，
又
，则
，代入上述方程可得
，
，则
，
设直线
的方程为
，同理可得
，
直线
的斜率为
，
直线
的斜率为
，
.
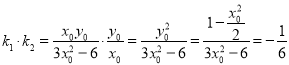所以，直线
与
的斜率之积为定值
，即
.
【题型】解答题
【结束】
21
【题目】已知函数
， 
，在
处的切线方程为
.
（1）求
， 
；
（2）若
，证明： 
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
