
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
【答案】
(1)解:∵f(x)是定义域为R的奇函数,∴f(0)=0,可k﹣1=0,即k=1,
故f(x)=ax﹣a﹣x(a>0,且a≠1)
∵f(1)>0,∴a﹣ ![]() >0,又a>0且a≠1,∴a>1.
>0,又a>0且a≠1,∴a>1.
f′(x)=axlna+ ![]()
∵a>1,∴lna>0,而ax+ ![]() >0,
>0,
∴f′(x)>0,∴f(x)在R上单调递增
原不等式化为:f(x2+2x)>f(4﹣x),
∴x2+2x>4﹣x,即x2+3x﹣4>0
∴x>1或x<﹣4,
∴不等式的解集为{x|x>1或x<﹣4}
(2)解:∵f(1)= ![]() ,∴a﹣
,∴a﹣ ![]() =
= ![]() ,即2a2﹣3a﹣2=0,∴a=2或a=﹣
,即2a2﹣3a﹣2=0,∴a=2或a=﹣ ![]() (舍去).
(舍去).
∴g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.
令t=f(x)=2x﹣2﹣x,由(1)可知f(x)=2x﹣2﹣x为增函数
∵x≥1,∴t≥f(1)= ![]() ,
,
令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2 (t≥ ![]() )
)
若m≥ ![]() ,当t=m时,h(t)min=2﹣m2=﹣2,∴m=2
,当t=m时,h(t)min=2﹣m2=﹣2,∴m=2
若m< ![]() ,当t=
,当t= ![]() 时,h(t)min=
时,h(t)min= ![]() ﹣3m=﹣2,
﹣3m=﹣2,
解得m= ![]() >
> ![]() ,舍去
,舍去
综上可知m=2
【解析】(1)根据f(x)是定义域为R的奇函数,可得k=1,从而f(x)=ax﹣a﹣x(a>0,且a≠1),利用f(1)>0,可得a>1,从而可证f(x)在R上单调递增,故原不等式化为x2+2x>4﹣x,从而可求不等式的解集;(2)根据f(1)= ![]() 确定a=2的值,从而可得函数g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.令t=f(x)=2x﹣2﹣x , 由(1)可知f(x)=2x﹣2﹣x为增函数,可得t≥f(1)=
确定a=2的值,从而可得函数g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.令t=f(x)=2x﹣2﹣x , 由(1)可知f(x)=2x﹣2﹣x为增函数,可得t≥f(1)= ![]() ,令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2(t≥
,令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2(t≥ ![]() ),分类讨论,利用最小值为﹣2,可求m的值.
),分类讨论,利用最小值为﹣2,可求m的值.
【考点精析】根据题目的已知条件,利用奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于( ) 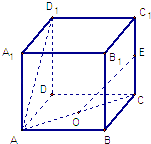
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是抛物线y2=8x上的一个动点,Q是圆(x﹣3)2+(y﹣1)2=1上的一个动点,N(2,0)是一个定点,则|PQ|+|PN|的最小值为( )
A.3
B.4
C.5
D.![]() +1
+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,t小时内供水总量为 ![]() 吨,(0≤t≤24)
吨,(0≤t≤24)
(1)从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣(m﹣1)x+2m
(1)若函数f(x)>0在(0,+∞)上恒成立,求m的取值范围;
(2)若函数f(x)在(0,1)内有零点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[﹣2,2]上的函数y=f(x)和y=g(x),其图象如图所示:给出下列四个命题:
①方程f[g(x)]=0有且仅有6个根 ②方程g[f(x)]=0有且仅有3个根
③方程f[f(x)]=0有且仅有5个根 ④方程g[g(x)]=0有且仅有4个根
其中正确命题的序号( )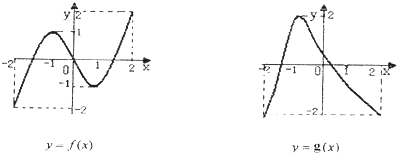
A.①②③
B.②③④
C.①②④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a∈R).
ax2﹣(2a+1)x+2lnx(a∈R).
(1)当a=1时,求函数f(x)的单调区间;
(2)当a>0时,设g(x)=(x2﹣2x)ex , 求证:对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是 ![]() ,D是AC的中点.
,D是AC的中点. 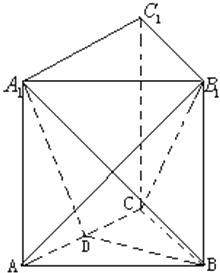
(1)求证:B1C∥平面A1BD;
(2)求二面角A1﹣BD﹣A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
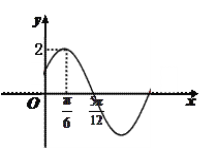
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com