
【题目】给定一个数列![]() ,在这个数列里,任取
,在这个数列里,任取![]() 项,并且不改变它们在数列
项,并且不改变它们在数列![]() 中的先后次序,得到的数列称为数列
中的先后次序,得到的数列称为数列![]() 的一个
的一个![]() 阶子数列.
阶子数列.
已知数列![]() 的通项公式为
的通项公式为![]() (
(![]() 为常数),等差数列
为常数),等差数列![]() 是
是
数列![]() 的一个3阶子数列.
的一个3阶子数列.
(1)求![]() 的值;
的值;
(2)等差数列![]() 是
是![]() 的一个
的一个![]() 阶子数列,且
阶子数列,且
![]() (
(![]() 为常数,
为常数,![]() ,求证:
,求证:![]() ;
;
(3)等比数列![]() 是
是![]() 的一个
的一个![]() 阶子数列,
阶子数列,
求证:![]() .
.
【答案】(1)0;(2)证明见解析;(3)证明见解析.
【解析】
试题(1)由![]() 成等差数列得
成等差数列得![]() ,可解得
,可解得![]() ;(2)
;(2)![]() 是等差数列,由
是等差数列,由![]() ,知
,知![]() ,从而
,从而![]() ,这样数列
,这样数列![]() 是递减的,但它是
是递减的,但它是![]() 的子数列,因此各项就均为正,由此有
的子数列,因此各项就均为正,由此有![]() ,从而有
,从而有![]() ,可得结论;(3)与(2)设
,可得结论;(3)与(2)设![]() ,类似得
,类似得![]() ,从而
,从而![]() ,
,![]() =
=![]() =
=![]() .下面要证
.下面要证![]() ,这可由证明函数
,这可由证明函数![]() 的单调性得其最大值得到结论.
的单调性得其最大值得到结论.
试题解析:(1)因为![]() 成等差数列,所以
成等差数列,所以![]() .
.
又因为![]() ,
,![]() ,
,![]() ,
,
代入得![]() ,解得
,解得![]() .
.
(2)设等差数列![]() 的公差为
的公差为![]() .
.
因为![]() ,所以
,所以![]() ,
,
从而![]() .
.
所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
即![]() .所以
.所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
(3)设![]() (
(![]() ),等比数列
),等比数列![]() 的公比为
的公比为![]() .
.
因为![]() ,所以
,所以![]() .
.
从而![]() .
.
所以![]()
=![]()
=![]() .
.
设函数![]() .
.
当![]() 时,函数
时,函数![]() 为单调增函数.
为单调增函数.
因为当![]() ,所以
,所以![]() .所以
.所以![]() .
.
即![]() .
.
【注:若有其它解法,请酌情给分】


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点
,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点![]() 不含端点A,B,
不含端点A,B,![]() ,且
,且![]() ,则
,则![]() 的最大值为______.
的最大值为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校抽取了100名学生期中考试的英语和数学成绩,已知成绩都不低于100分,其中英语成绩的频率分布直方图如图所示,成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
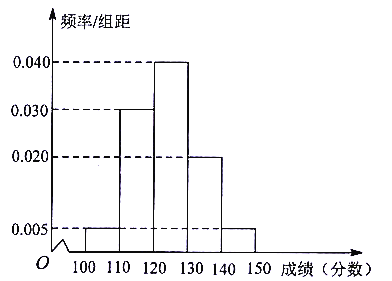
(1)根据频率分布直方图,估计这100名学生英语成绩的平均数和中位数(同一组数据用该区间的中点值作代表);
(2)若这100名学生数学成绩分数段的人数y的情况如下表所示:
分组区间 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且区间![]() 内英语人数与数学人数之比为
内英语人数与数学人数之比为![]() ,现从数学成绩在
,现从数学成绩在![]() 的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在
的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 和
和![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列三个命题:
变化时,给出下列三个命题:
①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②
轴对称;②![]() 的最小值为2;
的最小值为2;
③存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个,
仅有两个,
其中,所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出100户调查社会购买力的某一项指标,应采用的最佳抽样方法是分层抽样
②线性回归直线![]() 一定过样本中心点
一定过样本中心点![]()
③对于一组数据![]() ,如果将它们改变为
,如果将它们改变为![]() ,则平均数与方差均发生变化
,则平均数与方差均发生变化
④若一组数据1、![]() 、2、3的众数是2,则这组数据的中位数是2
、2、3的众数是2,则这组数据的中位数是2
⑤用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为76
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 与
与![]() 的中心在坐标原点
的中心在坐标原点![]() ,长轴均为
,长轴均为![]() 且在
且在![]() 轴上,短轴长分别为
轴上,短轴长分别为![]() ,
,![]() ,过原点且不与
,过原点且不与![]() 轴重合的直线
轴重合的直线![]() 与
与![]() ,
,![]() 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为![]() ,记
,记![]() ,
,![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() .
.
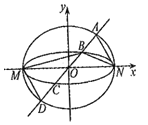
(1)当直线![]() 与
与![]() 轴重合时,若
轴重合时,若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线![]() ,使得
,使得![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com