练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数有两个零点．

    （1）若函数的两个零点是和，求的值，并写出不等式的解集；

    （2）当时，函数有两个零点和，求的取值范围．

    【答案】（1）,解集为,（2）

    【解析】

    （1）根据题意，得到和是方程的两个实数根，由此，列出方程组求解，得出，再解不等式，即可得出结果.

    （2）根据题意，得到和是方程的两根，由根与系数关系，得到，根据二次函数性质，以及题中条件，即可求出结果.

    （1）∵和是函数的两个零点，

    ∴和是方程的两个实数根，

    ∴解得．

    所以，

    因此不等式即为，解得：；

    ∴不等式的解集为．

    （2）因为函数的两个零点为和，

    则和是方程的两根，

    ∴，

    ∴，

    因为，是开口向下，对称轴为的二次函数

    ∴在区间上单调递减，

    因此，，

    即的最大值为，最小值是，

    所以的取值范围为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知对数函数过点，.

    （1）求的解析式，并指出的定义域；

    （2）设，求函数的零点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AD⊥平面PCD，PD⊥CD，底面ABCD是梯形，AB∥DC，AB=AD=PD=1，CD=2AB， 为棱PC上一点.

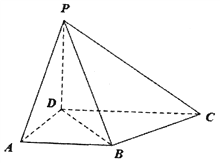
    (Ⅰ)若点是PC的中点，证明：B∥平面PAD；

    (Ⅱ) 试确定的值使得二面角-BD-P为60°.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】当生物死亡后,其体内原有的碳14的含量大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”．2019年7月6日，第43届世界遗产大会宣布，中国良渚古城遗址成功申遗，获准列入世界遗产名录．目前中国世界遗产总数已达55处，位居世界第一．今年暑期，某中学的“考古学”兴趣小组对良渚古城水利系统中一条水坝的建筑材料(草裹泥)上提取的草茎遗存进行碳14年代学检测，检测出碳14的残留量约为初始量的54%．利用参考数据：，请你推断上述所提取的草茎遗存物距今大约有_______________________年（精确到1年）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．

    求证：（1）A1B1∥平面DEC1；

    （2）BE⊥C1E．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）的最小值为1，且f（0）＝f（2）＝3．

    （1）求f（x）的解析式；

    （2）若f（x）在区间[2a，a+1]上不单调，求实数a的取值范围；

    （3）在区间[﹣1，1]上，y＝f（x）的图象恒在y＝2x+2m+1的图象上方，试确定实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新一届中央领导集体非常重视勤俭节约，从“光盘行动”到“节约办春晚”．到饭店吃饭是吃光盘子或时打包带走，称为“光盘族”，否则称为“非光盘族”．政治课上政治老师选派几位同学组成研究性小组，从某社区[25,55]岁的人群中随机抽取人进行了一次调查，得到如下统计表：

    组数

    分组

    频数

    频率

    光盘族占本组比例

    第1组

    [25,30）

    50

    0．05

    30%

    第2组

    [30,35）

    100

    0．10

    30%

    第3组

    [35,40）

    150

    0．15

    40%

    第4组

    [40,45）

    200

    0．20

    50%

    第5组

    [45,50）

    a

    b

    65%

    第6组

    [50,55）

    200

    0．20

    60%

    （1）求的值，并估计本社区[25,55）岁的人群中“光盘族”所占比例；

    （2）从年龄段在[35,45）的“光盘族”中采用分层抽样方法抽取8人参加节约粮食宣传活动，并从这8人中选取2人作为领队．求选取的2名领队分别来自[35,40）与[40,45）两个年龄段的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一则“清华大学要求从 2017级学生开始，游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.其实，已有不少高校将游泳列为必修内容.

    某中学拟在高一-下学期开设游泳选修课，为了了解高--学生喜欢游泳是否与性别有关，该学校对100名高一新生进行了问卷调查，得到如下列联表:

    喜欢游泳

    不喜欢游泳

    合计

    男生

    40

    女生

    30

    合计

    已知在这100人中随机抽取1人，抽到喜欢游泳的学生的概率为.

    (1).请将上述列联表补充完整，并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.

    (2)已知在被调查的学生中有6名来自高一(1) 班，其中4名喜欢游泳，现从这6名学生中随机抽取2人，求恰有1人喜欢游泳的概率.

    附：

    0.10

    0.050

    0.025

    0.010

    0.005

    0.001

    2.706

    /td>

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近期，济南公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用表示活动推出的天数, 表示每天使用扫码支付的人次(单位:十人次),统计数据如表所示:

    根据以上数据,绘制了散点图.

    (1)根据散点图判断,在推广期内, 与(均为大于零的常数)哪一个适宜作为扫码支付的人次关于活动推出天数的回归方程类型?(给出判断即可,不必说明理由);

    (2)根据(1)的判断结果及表中的数据,建立关于的回归方程,并预测活动推出第天使用扫码支付的 人次；

    (3)推广期结束后,车队对乘客的支付方式进行统计，结果如下

    车队为缓解周边居民出行压力,以万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为万元.已知该线路公交车票价为元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受折优惠,扫码支付的乘客随机优惠，根据统计结果得知,使用扫码支付的乘客中有的概率享受折优惠,有的概率享受折优惠,有的概率享受折优惠.预计该车队每辆车每个月有万人次乘车,根据给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要年才能开始盈利,求的值.

    参考数据:

    其中其中

    参考公式:

    对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为: .

    查看答案和解析>>

    同步练习册答案