练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=x2﹣ x+ ，若数列{bn}满足：b1=1，bn+1=2f（bn）（n∈N*）．若对n∈N* ， 都M∈Z，使得 ＜M恒成立，则整数M的最小值是（ ）
    A.2
    B.3
    C.4
    D.5

    【答案】A
    【解析】解：函数f（x）=x2﹣ x+ ， ∴bn+1=2f（bn）=2bn2﹣bn+ ，
    ∴2bn+1=4bn2﹣2bn+1，
    ∴2bn+1=2bn（2bn﹣1）+1
    ∴2bn+1﹣1=2bn（2bn﹣1），
    ∴ = = ﹣
    ∴ = ﹣ ，
    ∴ （ ）= ﹣ + + + ﹣ =1﹣ ，
    ∴ =2（1﹣ ），
    由f（x）=x2﹣ x+ 可知bn为增数列，且b1=1，
    ∴2（1﹣ ）＜2，
    故整数M的最小值是2，
    故选：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某班有学生50人，其中男同学30人，用分层抽样的方法从该班抽取5人去参加某社区服务活动．
    （1）求从该班男女同学在各抽取的人数；
    （2）从抽取的5名同学中任选2名谈此活动的感受，求选出的2名同学中恰有1名男同学的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩（单位：分）．已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x、y的值分别为（ ）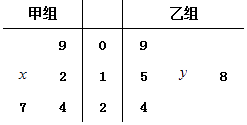

    A.2，5
    B.5，5
    C.5，8
    D.8，8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点．求证：
    （1）PA∥平面BDE；
    （2）BD⊥平面PAC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若圆的一条直径的两个端点分别是（﹣1，3）和（5，﹣5），则此圆的方程是（ ）
    A.x2+y2+4x+2y﹣20=0
    B.x2+y2﹣4x﹣2y﹣20=0
    C.x2+y2﹣4x+2y+20=0
    D.x2+y2﹣4x+2y﹣20=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线l过直线x+y﹣2=0和直线x﹣y+4=0的交点，且与直线3x﹣2y+4=0平行，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的顶点A（5，1），AB边上的中线CM所在直线方程为2x﹣y﹣5=0，∠B的平分线BN所在直线方程为x﹣2y﹣5=0．求：
    （1）顶点B的坐标；
    （2）直线BC的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的定义域为集合A，函数g（x）=lg（x2﹣2x+a）的定义域为集合B． （Ⅰ）当a=﹣8时，求A∩B；
    （Ⅱ）若A∩RB={x|﹣1＜x≤3}，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中， ，求b，c．

    查看答案和解析>>

    同步练习册答案