
【题目】已知点![]() ,圆
,圆![]() ,过点
,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)当![]() (
(![]() 不重合)时,求
不重合)时,求![]() 的方程及
的方程及![]() 的面积.
的面积.
【答案】(I)![]() ;(II)
;(II)![]() (或
(或![]() ) ,
) , ![]()
【解析】
(Ⅰ)由圆C的方程求出圆心坐标和半径,设出M坐标,由![]() 与
与![]() 数量积等于0列式得M的轨迹方程;
数量积等于0列式得M的轨迹方程;
(Ⅱ)设M的轨迹的圆心为N,由|OP|=|OM|得到ON⊥PM.求出ON所在直线的斜率,由直线方程的点斜式得到PM所在直线方程,由点到直线的距离公式求出O到l的距离,再由弦心距、圆的半径及弦长间的关系求出PM的长度,代入三角形面积公式得答案.
(I)圆C的方程可化为![]() ,∴圆心为
,∴圆心为![]() ,半径为4,设
,半径为4,设![]() ,
,
∴![]() 由题设知
由题设知![]()
![]() ,即
,即![]() .由于点
.由于点![]() 在圆
在圆![]() 的内部,所以
的内部,所以![]() 的轨迹方程是
的轨迹方程是![]() .
.
(II)由(I)可知![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,
为圆心,![]() 为半径的圆.
为半径的圆.
由于![]() ,故
,故![]() 在线段
在线段![]() 的垂直平分线上,又
的垂直平分线上,又![]() 在圆
在圆![]() 上,从而
上,从而![]() .
.
∵![]() 的斜率为3
的斜率为3![]()
![]() ∴
∴![]() 的方程为
的方程为![]() .(或
.(或![]() ).又
).又![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,∴
,∴![]() 的面积为
的面积为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸x(mm)之间近似满足关系式
与尺寸x(mm)之间近似满足关系式![]() (b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
(b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸x(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量y (g) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(Ⅰ)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(ⅰ)根据所给统计量,求y关于x的回归方程;
(ⅱ)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸x为何值时,收益
,则当优等品的尺寸x为何值时,收益![]() 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)
附:对于样本![]()
![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
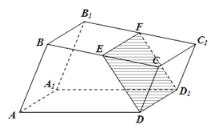
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 是圆心为
是圆心为![]() 半径为
半径为![]() 的半圆弧上从点
的半圆弧上从点![]() 数起的第一个三等分点,点
数起的第一个三等分点,点![]() 是圆心为
是圆心为![]() 半径为
半径为![]() 的半圆弧的中点,
的半圆弧的中点,![]() 、
、![]() 分别是两个半圆的直径,
分别是两个半圆的直径,![]() ,直线
,直线![]() 与两个半圆所在的平面均垂直,直线
与两个半圆所在的平面均垂直,直线![]() 、
、![]() 共面.
共面.

(1)求三棱锥![]() 的体积;
的体积;
(2)求直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点且
两点且![]() .求证:
.求证: ![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某菜园要将一批蔬菜用汽车从所在城市甲运至亚运村乙,已知从城市甲到亚运村乙只有两条公路,且运费由菜园承担.
若菜园恰能在约定日期(![]() 月
月![]() 日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.
日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.
为保证蔬菜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送蔬菜,已知下表内的信息:
统计信息 | 不堵车的情况下到达亚运村乙所需 时间 (天) | 堵车的情况下到达亚运村乙所需时间 (天) | 堵车的 | 运费 |
公路1 | 2 | 3 |
|
|
公路2 | 1 | 4 |
|
|
(注:毛利润![]() 销售商支付给菜园的费用
销售商支付给菜园的费用![]() 运费)
运费)
(Ⅰ) 记汽车走公路1时菜园获得的毛利润为![]() (单位:万元),求
(单位:万元),求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅱ) 假设你是菜园的决策者,你选择哪条公路运送蔬菜有可能让菜园获得的毛利润更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学理科成绩优异,今年参加了数学,物理,化学,生物4门学科竞赛.已知该同学数学获一等奖的概率为![]() ,物理,化学,生物获一等奖的概率都是
,物理,化学,生物获一等奖的概率都是![]() ,且四门学科是否获一等奖相互独立.
,且四门学科是否获一等奖相互独立.
(1)求该同学至多有一门学科获得一等奖的概率;
(2)用随机变量![]() 表示该同学获得一等奖的总数,求
表示该同学获得一等奖的总数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 满足:
满足:![]() ,
,![]() .
.![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)若![]() ,
,![]() (
(![]() ),求数列
),求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() =
=![]()
【解析】
试题分析:(Ⅰ)设出首项a1和公差d ,利用等差数列通项公式,就可求出![]() ,再利用等差数列前项求和公式就可求出
,再利用等差数列前项求和公式就可求出![]() ;(Ⅱ)由(Ⅰ)知
;(Ⅱ)由(Ⅰ)知![]() ,再利用
,再利用![]() ,
,![]() (
(![]() ),就可求出
),就可求出![]() ,再利用错位相减法就可求出
,再利用错位相减法就可求出![]() .
.
试题解析:(Ⅰ)设等差数列{an}的首项为a1,公差为d
∵ ![]() ,
,![]() ∴
∴ ![]() 解得
解得 ![]()
∴ ![]()
![]() ,
,
(Ⅱ)∵ ![]() ,
,![]() ∴
∴ ![]()
∵![]() ∴
∴ ![]()
∴ ![]()
![]()
![]()
= ![]() (1-
(1- ![]() +
+ ![]() -
- ![]() +…+
+…+![]() -
-![]() )
)
=![]() (1-
(1-![]() ) =
) =![]()
所以数列![]() 的前
的前![]() 项和
项和![]() =
=![]() .
.
考点:1.等差数列的通项公式; 2. 等差数列的前n项和公式; 3.裂项法求数列的前n项和公式
【题型】解答题
【结束】
18
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
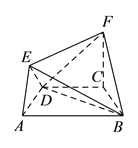
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com