
【题目】已知函数![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)设函数![]()
![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() (2)当
(2)当![]() 时,
时,![]() 有0个零点;当
有0个零点;当![]() 或
或![]() 时,
时,![]() 有1个零点;当
有1个零点;当![]() 时,
时,![]() 有2个零点.
有2个零点.
【解析】
(1)令![]() 求导,令
求导,令![]() ,求出
,求出![]() 的值,进而求出单调区间,极小值,求出最小值;
的值,进而求出单调区间,极小值,求出最小值;
(2)求![]() ,求出单调区间和极值,得出
,求出单调区间和极值,得出![]() ,
,![]() 等价转化为
等价转化为![]() ,转化为求直线
,转化为求直线![]() 与函数
与函数![]() 的图像交点个数,通过求导数的方法,研究函数
的图像交点个数,通过求导数的方法,研究函数![]() 的单调区间,极值和图像变化趋势,即可求解.
的单调区间,极值和图像变化趋势,即可求解.
解:(1)令![]()
![]() ,
,
令![]() ,
,![]() ,
,
所以![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ,
,
所以![]() 时,
时,![]() 取得极小值,也是最小值,
取得极小值,也是最小值,
所以![]() ;
;
(2)![]() ,令
,令![]() ,
,
![]()
![]() 的递减区间是
的递减区间是![]() ,递增区间是
,递增区间是![]() ,
,
所以![]() 的极小值为
的极小值为![]() ,也是最小值,
,也是最小值,![]() .
.
所以![]()
![]() ,
,
因为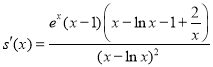 ,
,
令![]()
![]() ,
,
令![]() ,
,![]()
![]() 的递减区间是
的递减区间是![]() ,递增区间是
,递增区间是![]() ,
,
所以![]() 的极小值为
的极小值为![]() ,也是最小值,
,也是最小值,
所以![]() ,
,
所以![]() 的递减区间是
的递减区间是![]() ,递增区间是
,递增区间是![]() ,
,
又因为![]()
![]()
![]()
![]() ,且
,且![]() ,
,
所以,当![]() 时,
时,![]() 有0个零点;
有0个零点;
当![]() 或
或![]() 时,
时,![]() 有1个零点;
有1个零点;
当![]() 时,
时,![]() 有2个零点.
有2个零点.


科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新的劳动合同法出台后,某公司实行了年薪制工资结构改革.该公司从2008年起,每人的工资由三个项目构成,并按下表规定实施:
项目 | 金额[元/(人年)] | 性质与计算方法 |
基础工资 | 2007年基础工资为20000元 | 考虑到物价因素,决定从2008年 起每年递增10%(与工龄无关) |
房屋补贴 | 800 | 按职工到公司年限计算,每年递增800元 |
医疗费 | 3200 | 固定不变 |
如果该公司今年有5位职工,计划从明年起每年新招5名职工.
(1)若今年算第一年,将第n年该公司付给职工工资总额y(万元)表示成年限n的函数;
(2)若公司每年发给职工工资总额中,房屋补贴和医疗费的总和总不会超过基础工资总额的p%,求p的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,
,![]() 为抛物线上在第一象限内一点,
为抛物线上在第一象限内一点,![]() 为原点,
为原点,![]() 面积为
面积为![]() .
.
(1)求抛物线方程;
(2)过![]() 点作两条直线分别交抛物线于异于点
点作两条直线分别交抛物线于异于点![]() 的两点
的两点![]() ,
,![]() ,且两直线斜率之和为
,且两直线斜率之和为![]() ,
,
(i)若![]() 为常数,求证直线
为常数,求证直线![]() 过定点
过定点![]() ;
;
(ii)当![]() 改变时,求(i)中距离
改变时,求(i)中距离![]() 最近的点
最近的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=cos(asinx)﹣sin(bcosx)没有零点,则a2+b2的取值范围是( )
A.[0,1)B.[0,π2)C.![]() D.[0,π)
D.[0,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD为直角梯形,AD//BC,∠SAD =∠DAB=![]() ,SA=3,SB=5,
,SA=3,SB=5,![]() ,
,![]() ,
,![]() .
.
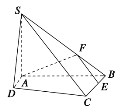
(1)求证:AB![]() 平面SAD;
平面SAD;
(2)求平面SCD与平面SAB所成的锐二面角的余弦值;
(3)点E,F分别为线段BC,SB上的一点,若平面AEF//平面SCD,求三棱锥B-AEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 进行翻折,得到三棱锥
进行翻折,得到三棱锥![]() ,则在翻折的过程中,有下列结论正确的有_____.
,则在翻折的过程中,有下列结论正确的有_____.
①三棱锥![]() 的体积的最大值为
的体积的最大值为![]() ;
;
②三棱锥![]() 的外接球体积不变;
的外接球体积不变;
③三棱锥![]() 的体积最大值时,二面角
的体积最大值时,二面角![]() 的大小是60°;
的大小是60°;
④异面直线![]() 与
与![]() 所成角的最大值为90°.
所成角的最大值为90°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,C、D两点的坐标为
为坐标原点,C、D两点的坐标为![]() ,曲线
,曲线![]() 上的动点P满足
上的动点P满足![]() .又曲线
.又曲线![]() 上的点A、B满足
上的点A、B满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点A在第一象限,且![]() ,求点A的坐标;
,求点A的坐标;
(3)求证:原点到直线AB的距离为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com