
 ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2
ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
|
4
| ||
| m |
| OF |
| FQ |
| x2 |
| a2 |
| y2 |
| b2 |
| FQ |
| 1 |
| 2 |
| OF |
| 6 |
4
| ||
| c |
| ||
| 4 |
| OQ |
|
|
| 12 |
| 3 |
| 3 |
| 3 |
| 3 |
| (x1-x2)2+(y1-y2)2 |
|
4
| ||
| m |
| 6 |
| 6 |
| ¦Đ |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| FQ |
| 1 |
| 2 |
| OF |
| 6 |
4
| ||
| c |
| ||
| 4 |
| ||
| 4 |
| OQ |
|
|
| 12 |
| OQ |
| 6 |
| 6 |
| 6 |
| 6 |
|
|
| x2 |
| 4 |
| y2 |
| 12 |
| 3 |
| 3 |
| 3 |
| 3 |
| (x1-x2)2+(y1-y2)2 |
| (x1-x2)2+(y1-y2)2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2y | ||
|
| 3 |
| 2y | ||
|
| 3 |
| y2 |
| 300 |
| x2 | ||
|



| Ä꼶 | ¸ßÖĐżÎłĚ | Ä꼶 | łőÖĐżÎłĚ |
| ¸ßŇ» | ¸ßŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ | łőŇ» | łőŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ß¶ţ | ¸ß¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ | łő¶ţ | łő¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ßČý | ¸ßČýĂâ·ŃżÎłĚÍĆĽöŁˇ | łőČý | łőČýĂâ·ŃżÎłĚÍĆĽöŁˇ |
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
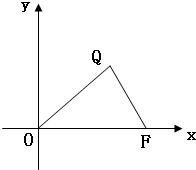 ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2
ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
 ČçÍĽŁ¬ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞSŁ¬ÇŇ
ČçÍĽŁ¬ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞSŁ¬ÇŇ| OF |
| FQ |
| 1 |
| 2 |
| ||
| 2 |
| OF |
| FQ |
| OF |
| 3 |
| 4 |
| OQ |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
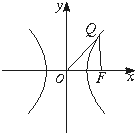 ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2
ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
 Ł¨2007•Ěě˝ňһģŁ©ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2
Ł¨2007•Ěě˝ňһģŁ©ŇŃÖŞˇ÷OFQµÄĂć»ýÎŞ2| 6 |
| OF |
| FQ |
| 2 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
˛éż´´đ°¸şÍ˝âÎö>>
°Ů¶ČÖÂĐĹ - Á·Ď°˛áÁбí - ĘÔĚâÁбí
şţ±±Ęˇ»ĄÁŞÍřÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨Ć˝Ě¨ | ÍřÉĎÓĐş¦ĐĹϢľŮ±¨×¨Çř | µçĐĹթƾٱ¨×¨Çř | ÉćŔúĘ·ĐéÎŢÖ÷ŇĺÓĐş¦ĐĹϢľŮ±¨×¨Çř | ÉćĆóÇÖȨľŮ±¨×¨Çř
ÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨µç»°Łş027-86699610 ľŮ±¨ÓĘĎ䣺58377363@163.com