
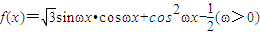 ,其最小正周期为
,其最小正周期为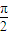 .
. 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间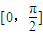 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.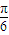 ),再根据它的最小正周期为
),再根据它的最小正周期为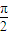 ,求得ω=2,从而求得f(x)的表达式.
,求得ω=2,从而求得f(x)的表达式.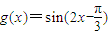 ,由题意可得函数y=g(x)与y=k在区间[0,
,由题意可得函数y=g(x)与y=k在区间[0,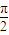 ]上有且只有一个交点,结合正弦函数的图象求得实数k的取值范围.
]上有且只有一个交点,结合正弦函数的图象求得实数k的取值范围.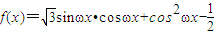 =
=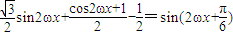 .…(3分)
.…(3分)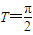 ,
,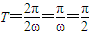 ,所以ω=2…(5分)
,所以ω=2…(5分)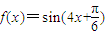 …(6分)
…(6分)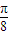 个单位后,得到
个单位后,得到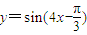 的图象,
的图象,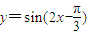 的图象.
的图象.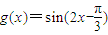 …(9分)
…(9分)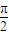 ,所以
,所以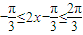 .
. ]上有且只有一个实数解,即函数y=g(x)与y=k在区间[0,
]上有且只有一个实数解,即函数y=g(x)与y=k在区间[0,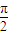 ]上有且只有一个交点,
]上有且只有一个交点,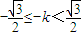 ,或k=-1,
,或k=-1,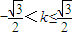 ,或k=-1.…(12分)
,或k=-1.…(12分)

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
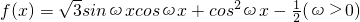 ,其最小正周期为
,其最小正周期为 .
. 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,其最小正周期为
,其最小正周期为![]()
(I)求![]() 的表达式;
的表达式;
(II)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() ,在区间
,在区间![]() 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,其最小正周期为
,其最小正周期为![]()
(I)求![]() 的表达式;
的表达式;
(II)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() ,在区间
,在区间![]() 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013年山东省淄博市高考数学二模试卷(理科)(解析版) 题型:解答题
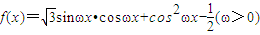 ,其最小正周期为
,其最小正周期为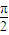 .
.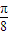 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间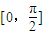 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com