
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.48 | 1.47 | 1.53 | 1.52 | 1.47 |
分析 (1)由条件利用古典概率及其计算公式,求得从10个零件中,随机抽取一个为一等品的概率.
(2)①设一等品零件的编号为A1、A2、A3、A4、A5,从这5个一等品零件中随机抽取2个,所有可能的结果用列举法求得共有10个.
②设“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果用列举法求得共有4个,可得从一等品零件中,随机抽取的2个零件直径相等概率.
(3)由(2)知甲、乙分别从一等品中各取一个,共有20种可能(有序),而甲取到零件的直径大于乙取到零件的直径的有6种可能.由此求得甲取到零件的直径大于乙取到零件的直径的概率.
解答 解:(1)由所给数据可知,一等品零件共有5个,设“从10个零件中,随机抽取一个为一等品”为事件A,
则p(A)=$\frac{5}{10}$=$\frac{1}{2}$.
所以,从10个零件中,随机抽取一个为一等品的概率为$\frac{1}{2}$.
(2)①解:一等品零件的编号为A1、A2、A3、A4、A5,从这5个一等品零件中随机抽取2个,所有可能的结果有:
A1、A2; A1、A3; A1、A4; A1、A5; A2、A3; A2、A4; A2、A5; A3、A4; A3、A5;A4、A5,共计10个.
②解“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:A1、A4;
A2、A3; A2、A5;A3、A5,共有4种.
故从一等品零件中,随机抽取的2个零件直径相等概率为$\frac{4}{10}$=$\frac{2}{5}$.
(3)由(2)知甲、乙分别从一等品中各取一个,共有20种可能(有序),
甲取到零件的直径大于乙取到零件的直径的有6种可能.
记“甲取到零件的直径大于乙取到零件的直径”为事件C,则甲取到零件的直径大于乙取到零件的直径的概率为$\frac{6}{20}$=$\frac{3}{10}$.
点评 本题主要考查古典概率及其计算公式,等可能事件的概率,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
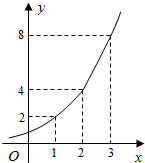 如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
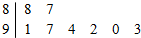 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91.5、5 | B. | 91、5 | C. | 92、5.5 | D. | 92、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com