
设![]() 是函数
是函数![]() 的一个极值点。
的一个极值点。
(Ⅰ)、求![]() 与
与![]() 的关系式(用
的关系式(用![]() 表示
表示![]() ),并求
),并求![]() 的单调区间;
的单调区间;
(Ⅱ)、设![]() ,
,![]() 。若存在
。若存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
点评:本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力。
解:(Ⅰ)![]() =-[x2+(a-2)x+b-a ]e3-x,
=-[x2+(a-2)x+b-a ]e3-x,
由![]() =0,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
=0,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
则 ![]() =[x2+(a-2)x-3-2a-a ]e3-x
=[x2+(a-2)x-3-2a-a ]e3-x
=-[x2+(a-2)x-3-3a ]e3-x
=-(x-3)(x+a+1)e3-x.
令![]() =0,得x1=3或x2=-a-1,由于x=3是极值点,
=0,得x1=3或x2=-a-1,由于x=3是极值点,
所以x+a+1≠0,那么a≠-4.
当a<-4时,x2>3=x1,则
在区间(-∞,3)上,![]() <0,
<0, ![]() 为减函数;
为减函数;
在区间(3,a1)上,![]() >0,
>0,![]() 为增函数;
为增函数;
在区间(a1,+∞)上,![]() <0,
<0,![]() 为减函数。
为减函数。
当a>-4时,x2<3=x1,则
在区间(-∞,a1)上,![]() <0,
<0, ![]() 为减函数;
为减函数;
在区间(a1,3)上,![]() >0,
>0,![]() 为增函数;
为增函数;
在区间(3,+∞)上,![]() <0,
<0,![]() 为减函数。
为减函数。
(Ⅱ)由(Ⅰ)知,当a>0时,![]() 在区间(0,3)上的单调递增,在区间(3,4)上单调递减,那么
在区间(0,3)上的单调递增,在区间(3,4)上单调递减,那么![]() 在区间[0,4]上的值域是[min(f (0),f (4) ),f (3)],
在区间[0,4]上的值域是[min(f (0),f (4) ),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f (3)=a+6,
那么![]() 在区间[0,4]上的值域是[-(2a+3)e3,a+6].
在区间[0,4]上的值域是[-(2a+3)e3,a+6].
又![]() 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是![]() ,
,
由于![]() ,所以只须仅须
,所以只须仅须
![]() 且a>0,解得
且a>0,解得![]() .
.
故a的取值范围是![]() 。
。


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
(09年莱西一中模拟理)(12分)
设![]() 是函数
是函数![]() 的一个极值点.
的一个极值点.
(Ⅰ)求![]() 与
与![]() 的关系式(用
的关系式(用![]() 表示
表示![]() ),并求
),并求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,使得
,使得![]() 成立?若存在,求
成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011届甘肃省兰州一中高三第三次模拟考试理科数学 题型:解答题
(本小题满分12分)
设 是函数
是函数 的一个极值点.
的一个极值点.
(1)求 与
与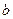 的关系式(用
的关系式(用 表示
表示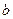 ),并求
),并求 的单调区间;
的单调区间;
(2)设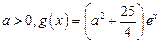 ,若存在
,若存在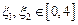 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟冲刺理科数学试卷(七)(解析版) 题型:解答题
设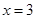 是函数
是函数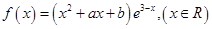 的一个极值点。
的一个极值点。
(1)求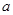 与
与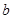 的关系式(用
的关系式(用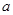 表示
表示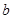 ),并求
),并求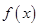 的单调区间;
的单调区间;
(2)设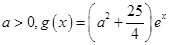 ,若存在
,若存在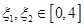 ,使得
,使得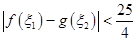 成立,求实数
成立,求实数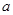 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年甘肃省高三第三次模拟考试理科数学 题型:解答题
(本小题满分12分)
设 是函数
是函数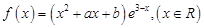 的一个极值点.
的一个极值点.
(1)求 与
与 的关系式(用
的关系式(用 表示
表示 ),并求
),并求 的单调区间;
的单调区间;
(2)设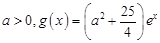 ,若存在
,若存在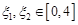 ,使得
,使得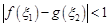 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com