
【题目】已知函数f(x)=sin(2ωx+![]() )+sin(2ωx-
)+sin(2ωx-![]() )+2cos2ωx,其中ω>0,且函数f(x)的最小正周期为π
)+2cos2ωx,其中ω>0,且函数f(x)的最小正周期为π
(1)求ω的值;
(2)求f(x)的单调增区间
(3)若函数g(x)=f(x)-a在区间[-![]() ,
,![]() ]上有两个零点,求实数a的取值范围.
]上有两个零点,求实数a的取值范围.
【答案】(1)1.(2) [-![]() +kπ,
+kπ,![]() +kπ],k∈Z,(3)见解析.
+kπ],k∈Z,(3)见解析.
【解析】
(1)利用三角函数恒等变换的应用化简函数解析式可得![]() ,利用三角函数周期公式可求
,利用三角函数周期公式可求![]() 的值.
的值.
(2)由正弦函数的单调性可求![]() 的单调增区间.
的单调增区间.
(3)作出函数![]() 在
在![]() 上的图象,从图象可看出
上的图象,从图象可看出![]()
![]() ,可求当曲线
,可求当曲线![]() 与
与![]() 在
在![]() ∈
∈![]() 上有两个交点时,2
上有两个交点时,2![]() ,即可得解实数
,即可得解实数![]() 的取值范围.
的取值范围.
(1)由三角恒等变换的公式,可得f(x)=sin(2![]() +
+![]() )+sin(2
)+sin(2![]() -
-![]() )+2
)+2![]()
=![]() sin2
sin2![]() +
+![]() cos2
cos2![]() +
+![]() sin2
sin2![]() -
-![]() cos2
cos2![]() +1+cos2
+1+cos2![]()
=sin2![]() +cos2
+cos2![]() +1
+1![]() ,
,
又因为T=![]() =π,所以
=π,所以![]() .
.
(2)由2kπ-![]()
![]() 2
2![]() +
+![]()
![]() 2kπ+
2kπ+![]() ,k∈Z,解得:-
,k∈Z,解得:-![]() +kπ
+kπ![]()
![]() +kπ,k∈Z,
+kπ,k∈Z,
可得f(x)的单调增区间为:[-![]() +kπ,
+kπ,![]() +kπ],k∈Z,
+kπ],k∈Z,
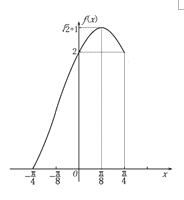
(3)作出函数![]() 在
在![]() 上的图象如图:
上的图象如图:
函数g(x)有两个零点,即方程![]() 有两解,
有两解,
亦即曲线![]() 与
与![]() 在x∈
在x∈![]() 上有两个交点,
上有两个交点,
从图象可看出f(0)=f(![]() )=2,f(
)=2,f(![]() )=
)=![]() +1,
+1,
所以当曲线![]() 与
与![]() 在x∈
在x∈![]() 上有两个交点时,
上有两个交点时,
则2![]()
![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知双曲线E: ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x. 
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() ;
;
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 上的距离的最小值的值.
上的距离的最小值的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
奖级 | 摸出红、蓝球个数 | 获奖金额 |
一等奖 | 3红1蓝 | 200元 |
二等奖 | 3红0蓝 | 50元 |
三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额x的分布列与期望E(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC,P0是边AB上一定点,满足 ![]() ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有 ![]() 则( )
则( )
A.∠ABC=90°
B.∠BAC=90°
C.AB=AC
D.AC=BC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1<x<6},B={x|2<x<10},C={x|5﹣a<x<a}.
(1)求A∪B,(RA)∩B;
(2)若CB,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com