
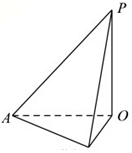
 如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )| A. | 20m | B. | 20$\sqrt{2}$m | C. | 20$\sqrt{3}$m | D. | 40m |
分析 设旗杆的高度为hm.依题意,可得PO⊥OA,PO⊥OB,由题意可得,OB=OP=h(m),OA=$\sqrt{3}$h,结合余弦定理,可得AB2=OA2+OB2-2OA•OBcos∠AOB可求h.
解答 解:设旗杆的高度为hm.依题意,可得PO⊥OA,PO⊥OB,
∴OB=OP=h(m),OA=$\sqrt{3}$h(m)
由余弦定理,可得AB2=OA2+OB2-2OA•OBcos∠AOB
即1600=3h2+h2-3h2,解得h=40(m)
∴旗杆的高度为40m.
故选D.
点评 本题主要考查了三角函数及余弦定理在解实际问题中的三角形中的应用,解题的关键是要把实际问题转化为数学中的三角形问题,属于解三角形在实际中的应用.


科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$或$\frac{3}{2}$ | B. | $\frac{3}{2}$或1 | C. | 1或$\frac{1}{2}$ | D. | $\frac{1}{2}$或$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,角A,B,C的对边分别为a,b,c,a2+b2+c2=ac+bc+ca.
在△ABC中,角A,B,C的对边分别为a,b,c,a2+b2+c2=ac+bc+ca.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
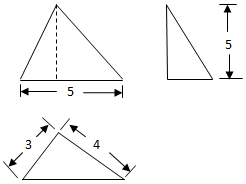
| A. | $4\sqrt{2}$ | B. | $\sqrt{34}$ | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于原点对称 | B. | 关于x轴对称 | C. | 关于y轴对称 | D. | 关于直线y=x对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com