
【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log ![]() (﹣x+1).
(﹣x+1).
(1)求f(x)的解析式;
(2)若f(a﹣1)<﹣1,求实数a的取值范围.
【答案】
(1)解:令x>0,则﹣x<0,f(﹣x)=log ![]() (x+1)=f(x)
(x+1)=f(x)
∴x>0时,f(x)=log ![]() (x+1),
(x+1),
则f(x)= 
(2)解:∵f(x)=log ![]() (﹣x+1)在(﹣∞,0]上为增函数,
(﹣x+1)在(﹣∞,0]上为增函数,
∴f(x)在(0,+∞)上为减函数
∵f(a﹣1)<﹣1=f(1)
∴|a﹣1|>1,
∴a>2或a<0
【解析】(1)根据函数奇偶性的性质即可求函数f(x)的解析式;(2)若f(a﹣1)<﹣1,将不等式进行转化即可求实数a的取值范围
【考点精析】本题主要考查了对数函数的单调性与特殊点的相关知识点,需要掌握过定点(1,0),即x=1时,y=0;a>1时在(0,+∞)上是增函数;0>a>1时在(0,+∞)上是减函数才能正确解答此题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2ax+b2≥0恒成立时的概率:
(1)当a,b均为整数时;
(2)当a,b均为实数时.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)= ![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①f(﹣x)+f(x)=0在x∈R时恒成立;
②函数f(x)的值域为(﹣1,1);
③若x1≠x2 , 则一定有f(x1)≠f(x2);
④函数g(x)=f(x)﹣x在R上有三个零点.
其中正确结论的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为: ![]() =1(a>0),其焦点在x轴上,离心率e=
=1(a>0),其焦点在x轴上,离心率e= ![]() .
.
(1)求该椭圆的标准方程;
(2)设动点P(x0 , y0)满足 ![]() ,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣
,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣ ![]() ,求证:x02+2y02为定值.
,求证:x02+2y02为定值.
(3)在(2)的条件下,问:是否存在两个定点A,B,使得|PA|+|PB|为定值?若存在,给出证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图 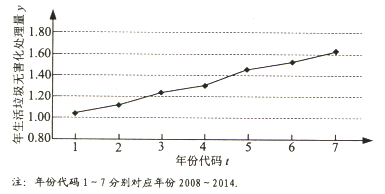
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: ![]() =9.32,
=9.32, ![]() yi=40.17,
yi=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:相关系数r= 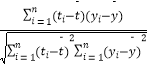 回归方程
回归方程 ![]() =
= ![]() +
+ ![]() t 中斜率和截距的最小二乘估计公式分别为:
t 中斜率和截距的最小二乘估计公式分别为: ![]() =
= 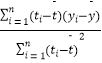 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对边分别是a、b、c,已知B=60°,
(1)若b= ![]() ,A=45°,求a;
,A=45°,求a;
(2)若a、b、c成等比数列,请判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中所有正确的序号是 .
①函数f(x)=ax﹣1+3(a>0且a≠1)的图象一定过定点P(1,4);
②函数f(x﹣1)的定义域是(1,3),则函数f(x)的定义域为(2,4);
③已知f(x)=x5+ax3+bx﹣8,且f(﹣2)=8,则f(2)=﹣8;
④f(x)= ![]() 为奇函数.
为奇函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com