
设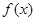 、
、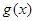 分别是定义在
分别是定义在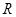 上的奇函数和偶函数,当
上的奇函数和偶函数,当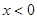 时,
时, ,且
,且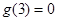 ,则不等式
,则不等式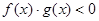 的解集是( )
的解集是( )
A.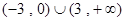 B.
B.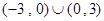
C.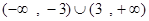 D.
D.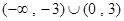
D
【解析】
试题分析:

解:设F(x)="f" (x)g(x),当x<0时,∵F′(x)=f′(x)g(x)+f (x)g′(x)>0.∴F(x)在当x<0时为增函数.∵F(-x)="f" (-x)g (-x)="-f" (x)?g (x)=-F(x).故F(x)为(-∞,0)∪(0,+∞)上的奇函数.∴F(x)在(0,∞)上亦为增函数.已知g(-3)=0,必有F(-3)=F(3)=0.构造如图的F(x)的图象,可知,F(x)<0的解集为x∈(-∞,-3)∪(0,3)故选D
考点:复合函数的求导运算
点评:本题主要考查复合函数的求导运算和函数的单调性与其导函数正负之间的关系.导数是一个新内容,也是高考的热点问题,要多注意复习


科目:高中数学 来源:2014届浙江省高二(9、10班)下期中考试数学卷(解析版) 题型:选择题
设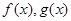 分别是定义在
分别是定义在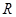 上的奇函数和偶函数,当
上的奇函数和偶函数,当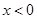 时,
时, 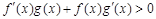 ,且
,且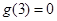 ,则不等式
,则不等式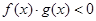 的解集是( )
的解集是( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)
C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省高三上学期第一次诊断性测试文科数学卷 题型:选择题
设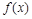 、
、 分别是定义在
分别是定义在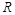 上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式
上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式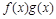 <0的解集是( )
<0的解集是( )
A.{x|-3<x<0或x>3} B.{x|x<-3或0<x<3}
C.{x|x<-3或x>3} D.{x|-3<x<0或0<x<3}
查看答案和解析>>
科目:高中数学 来源:2013届河南省高二3月月考理科数学试卷 题型:选择题
设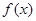 ,
,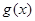 分别是定义在
分别是定义在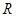 上的奇函数和偶函数,当
上的奇函数和偶函数,当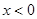 时,
时, ,且
,且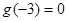 ,则不等式
,则不等式 的解集( )
的解集( )
A、 (-3,0)∪(3,+∞) B、(-3,0)∪(0,3)
C、 (-∞,-3)∪(3,+∞) D、 (-∞,-3)∪(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com