
【题目】(1)已知圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)已知圆![]() 与
与![]() 轴相切,圆心在直线
轴相切,圆心在直线![]() 上,且圆
上,且圆![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() ,求圆
,求圆![]() 的方程.
的方程.
【答案】(1)![]() ;
;
(2)![]() 或
或![]() .
.
【解析】
(1)求出过点![]() 且垂直于直线
且垂直于直线![]() 的直线方程,并求出线段
的直线方程,并求出线段![]() 的垂直平分线方程,联立两直线方程可得出圆心坐标,求出圆心到点
的垂直平分线方程,联立两直线方程可得出圆心坐标,求出圆心到点![]() 的距离作为圆的半径,由此可得出圆
的距离作为圆的半径,由此可得出圆![]() 的标准方程;
的标准方程;
(2)设圆心![]() 的坐标为
的坐标为![]() ,可知圆
,可知圆![]() 的半径为
的半径为![]() ,求出圆心
,求出圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,利用弦长的一半、
,利用弦长的一半、![]() 、圆的半径之间的关系并结合勾股定理求出
、圆的半径之间的关系并结合勾股定理求出![]() 的值,即可得出圆
的值,即可得出圆![]() 的标准方程.
的标准方程.
(1)由题意知圆心必在过切点![]() 且垂直切线
且垂直切线![]() 的直线上,
的直线上,
可求得此直线为![]() ,
,
直线![]() 的斜率为
的斜率为![]() ,线段
,线段![]() 的中点坐标为
的中点坐标为![]() ,则线段
,则线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,即
,即![]() ,
,
可知圆心必在线段![]() 的垂直平分线
的垂直平分线![]() 上,
上,
联立![]() ,可求得圆心
,可求得圆心![]() ,则
,则![]() ,
,
因此,圆![]() 的方程为
的方程为![]() ;
;
(2)设圆心![]() ,半径
,半径![]() ,
,
圆心到直线![]() 的距离为
的距离为![]() ,
,
由半弦长、弦心距、半径的关系得![]() ,
,![]() ,
,
当![]() 时,圆心
时,圆心![]() ,半径
,半径![]() ,此时圆
,此时圆![]() 为
为![]() ;
;
当![]() 时,圆心
时,圆心![]() ,半径
,半径![]() ,此时圆
,此时圆![]() 为
为![]() .
.
因此,圆![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
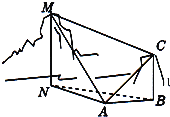
【题目】如图,为测量坡高MN,选择A和另一个山坡的坡顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知坡高BC=50米,则坡高MN=______米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.

现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中所有正确的序号是_________
①两直线的倾斜角相等,则斜率必相等;
②若动点![]() 到定点
到定点![]() 和定直线
和定直线![]() 的距离相等,则动点
的距离相等,则动点![]() 的轨迹是抛物线;
的轨迹是抛物线;
③已知![]() 、
、![]() 是椭圆
是椭圆![]() 的两个焦点,过点
的两个焦点,过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点,则
两点,则![]() 的周长为
的周长为![]() ;
;
④曲线的参数方程为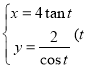 为参数
为参数![]() ,则它表示双曲线且渐近线方程为
,则它表示双曲线且渐近线方程为![]() ;
;
⑤已知正方形![]() ,则以
,则以![]() 、
、![]() 为焦点,且过
为焦点,且过![]() 、
、![]() 两点的椭圆的离心率为
两点的椭圆的离心率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)该种植基地在如图所示的长方形地块的每个格点(横纵直线的交点)处都种了一株该种水果,其中每个小正方形的面积都为![]() ,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知P是矩形ABCD所在平面上的一点,则有![]() .试证明该命题.
.试证明该命题.
(2)将上述命题推广到P为空间上任一点的情形,写出这个推广后的命题并加以证明.
(3)将矩形ABCD进一步推广到长方体![]() ,并利用(2)得到的命题建立并证明一个新命题.
,并利用(2)得到的命题建立并证明一个新命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)>3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤﹣1},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左、右顶点分别为A,B,离心率为
的左、右顶点分别为A,B,离心率为![]() ,点P(1,
,点P(1,![]() )为椭圆上一点.
)为椭圆上一点.

(1)求椭圆C的标准方程;
(2)如图,过点C(0,1)且斜率大于1的直线l与椭圆交于M,N两点,记直线AM的斜率为k1,直线BN的斜率为k2,若k1=2k2,求直线l斜率的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com