
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的零点,以及曲线
的零点,以及曲线![]() 在其零点处的切线方程;
在其零点处的切线方程;
(2)若方程![]() 有两个实数根
有两个实数根![]() ,求证:
,求证:![]() .
.
【答案】(1)零点为![]() ;
;![]() ;
;![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由题意可得函数![]() 的零点为
的零点为![]() ,
,![]() ,求导后,求出
,求导后,求出![]() ,
,![]() ,再求出
,再求出![]() ,利用点斜式即可求得切线方程;
,利用点斜式即可求得切线方程;
(2)利用导数证明![]() 、
、![]() ,设
,设![]() ,由函数单调性可知
,由函数单调性可知![]() 、
、![]() ,利用
,利用![]() 即可得证.
即可得证.
(1)由![]() ,得
,得![]() 或
或![]() ,所以函数
,所以函数![]() 的零点为
的零点为![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() .
.
又因为![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
在![]() 处的切线方程为
处的切线方程为![]() ;
;
(2)证明:因为函数![]() 的定义为
的定义为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() 即
即![]() 单调递减,
单调递减,
由![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
不妨设![]() ,且
,且![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
记![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 单调递增,且
单调递增,且![]() ,
,
故![]() 在
在![]() 单调递减,
单调递减,![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ;
;
记![]() ,则
,则![]() ,
,
所以![]() 单调递增,且
单调递增,且![]() ,故
,故![]() 在
在![]() 单减,
单减,![]() 在
在![]() 单增.
单增.
则![]() ,即
,即![]() ;
;
不妨设![]() ,
,
因为![]() ,且
,且![]() 为增函数,所以
为增函数,所以![]() .
.
由![]() ,得
,得![]() ;
;
同理![]() ,
,![]() ;
;
所以![]() .
.
所以![]() ,
,
所以![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,当几何体
折起,当几何体![]() 的的体积最大时,则下列命题中正确的个数是( )
的的体积最大时,则下列命题中正确的个数是( )

①![]()
②![]() ∥平面
∥平面![]()
③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角
所成的角
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() ,过点
,过点![]() 且与抛物线
且与抛物线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,弦
,弦![]() 和
和![]() 的中点分别为
的中点分别为![]() ,若
,若![]() ,则下列结论正确的是
,则下列结论正确的是
(______________)
①![]() 的最小值为32
的最小值为32
②以![]() 四点为顶点的四边形的面积的最小值为128
四点为顶点的四边形的面积的最小值为128
③直线![]() 过定点
过定点![]()
④焦点![]() 可以同时为弦
可以同时为弦![]() 和
和![]() 的三等分点
的三等分点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均为正实数,且满足a+b+c=m,求证:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由n(n∈N*)个正整数构成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),记SA=a1+a2+…+an,对于任意不大于SA的正整数m,均存在集合A的一个子集,使得该子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求证:“a1,a2,…,an成等差数列”的充要条件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值时an的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由![]() 个人依次出场解密,每人限定时间是
个人依次出场解密,每人限定时间是![]() 分钟内,否则派下一个人.
分钟内,否则派下一个人.![]() 个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲
个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲![]() 次的测试记录,绘制了如下的频率分布直方图.
次的测试记录,绘制了如下的频率分布直方图.
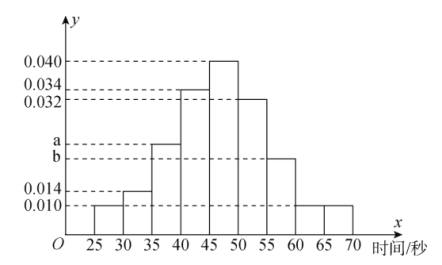
(1)若甲解密成功所需时间的中位数为![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分钟内解密成功的频率;
分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为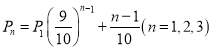 ,其中
,其中![]() 表示第
表示第![]() 个出场选手解密成功的概率,并且
个出场选手解密成功的概率,并且![]() 定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以![]() 从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目
从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,数列
,数列![]() 满足
满足![]() .
.
![]() Ⅰ
Ⅰ![]() 求数列
求数列![]() 和数列
和数列![]() 的通项公式;
的通项公式;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,若
,若![]() 对于一切的正整数
对于一切的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
![]() Ⅲ
Ⅲ![]() 数列
数列![]() 中是否存在
中是否存在![]() ,且
,且 ![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(consumer price index)的简称.居民消费价格指数是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.如图是根据国家统计局发布的2017年6月—2018年6月我国CPI涨跌幅数据绘制的折线图(注:2018年6月与2017年6月相比较,叫同比;2018年6月与2018年5月相比较,叫环比),根据该折线图,则下列结论错误的是( )
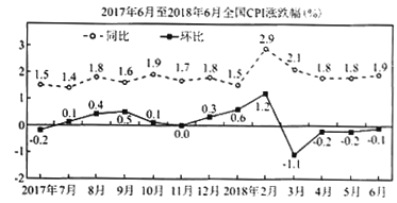
A.2017年8月与同年12月相比较,8月环比更大
B.2018年1月至6月各月与2017年同期相比较,CPI只涨不跌
C.2018年1月至2018年6月CPI有涨有跌
D.2018年3月以来,CPI在缓慢增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com